Mathematical thinking is the basis of all of the sciences. You cannot be a scientist without learning mathematical thinking.
Sam Nelson
Pero, ¿por qué?
Las matemáticas son especiales entre todas las áreas del conocimiento, pues en ellas se pueden hacer aseveraciones indudablemente verdaderas o completamente falsas. Para las otras ciencias, ya sean naturales o sociales, es inclusive peligroso afirmar que algo es cierto sin lugar a dudas. Dado lo anterior, quizá la única aseveración que se puede hacer con plena confianza es que toda persona que estudia, o estudió, matemáticas ha escuchado la frase «Yo odiaba las matemáticas» como respuesta casi inmediata al escuchar sobre su elección de carrera.
Las causas de esta repulsión visceral son múltiples, y las hojas de esta revista no alcanzarían para cubrir con detalle cada una de ellas. Sin embargo, aprovechemos este espacio para resaltar una de ellas: la ilusión de arbitrariedad. La justificación que gran parte de las personas que «odiaban las matemáticas» nos han dado se reduce a la idea de que las matemáticas son un conjunto de fórmulas y definiciones arbitrarias cuyo único propósito es ser memorizadas y regurgitadas en un examen. Concepción que, para los que hemos cursado alguna asignatura de matemáticas por los últimos cuatro años, suena diametralmente opuesta a la realidad.
¿Por qué es este el caso? Desde nuestra perspectiva, una de las características comunes a la mayoría de compañeros en la carrera es la curiosidad, esa molestia en la parte de atrás de la cabeza que no expira hasta que se pronuncian las palabras mágicas: «Pero, ¿por qué?». Y, solo hasta el momento en que se haya echado a andar esta curiosidad incisiva es que la ilusión de arbitrariedad comienza a resquebrajarse.
La maravilla de esta curiosidad es que se puede encender con cualquier pregunta. Para uno de nosotros, la primera instancia de curiosidad ocurrió cuando se le presentó la fórmula del volumen de una esfera: $V=\tfrac{4}{3} \pi r^3$. La aparición de $\pi$ y $r$ eran comunes y esperadas, pero «¿Por qué $\tfrac{4}{3}$?», preguntaba un pequeño estudiante de secundaria que esperaba ver un entero en vez de un racional en su fórmula. La confusión se volvió aún más grande cuando nadie supo decirle exactamente por qué $\tfrac{4}{3}$ era el coeficiente indicado para el volumen.
Imagínate la sorpresa del estudiante primerizo cuando finalmente llegó al curso de Cálculo Diferencial e Integral II y la gran revelación fue que $\tfrac{4}{3}$ era tan solo la constante de integración que resultaba de girar un círculo alrededor de un eje. Fue un momento menos climático de lo que aquel estudiante esperaba.
Pero, afortunadamente, las clases de universidad estuvieron repletas de momentos curiosos que resultaron ser más interesantes que éste. La lección es que la curiosidad a veces nos provee de mayor perspectiva sobre cómo operan los objetos con los que trabajamos, y otras veces a conclusiones poco emocionantes. Sin embargo, aún a pesar de la segunda posibilidad, creemos que fomentar la curiosidad es fundamental para romper el estigma social sobre las matemáticas.
¿$4\pi r^2$?

Regresemos a la esfera, la fórmula del volumen es parte del dominio público, pero la fórmula del área superficial es mucho menos conocida. Para una esfera de radio $r$, el área superficial de ésta está dada por la expresión
$$4 \pi r^2.\quad (1)$$
Vista de manera superficial esta expresión puede parecer tan arbitraria como todas las demás. Necesitamos una chispa para encender la curiosidad. Para un círculo de radio $r$, el área de dicha esfera se calcula mediante
$$\pi r^2 \quad (2)$$
Es aquí donde comienza la curiosidad.
¿Significa esto que una esfera tiene la misma área que cuatro círculos del mismo radio? Sí. ¿Entonces se puede construir una esfera utilizando solo cuatro círculos? Esta pregunta y la anterior no son tan distintas, pero la segunda requiere mayor atención. Antes de continuar leyendo toma un segundo y piensa cómo puede ser esto posible. Si tienes la oportunidad, forma círculos con papel o plastilina e intenta recrear una esfera de algún modo. Si tu acercamiento es pegar los círculos uno con otro, el hecho de que los círculos sean planos y la esfera causará problemas. Otro acercamiento puede ser cortar el círculo en partes más pequeñas e intentar reconstruir la esfera, pero la pregunta ahora se torna en cómo ordenar las piezas y ese es un problema aparte.
Los argumentos más comunes para afirmar que el área superficial de una esfera es $4 \pi r^2$, o sea, las demostraciones, usualmente utilizan herramientas de cálculo, por ejemplo, integración o proyección sobre un cilindro. Pero, aún cuando estas demostraciones explican por qué el área superficial es $4 \pi r^2$, ninguna de ellas hace evidente cómo cuatro círculos forman una esfera.
En otras palabras, ¿por qué el área superficial de una esfera igual a la de cuatro círculos? O, reinterpretando la pregunta, ¿por qué la superficie de una esfera es igual a 4 veces su sombra? [1] $($Figura 1$)$. La demostración que se desarrolla en el presente texto intenta responder a esta pregunta. Ciertamente no es la más «elegante», o la que usa las herramientas más sofisticadas, pero sí la que responde a la curiosidad.
La prueba
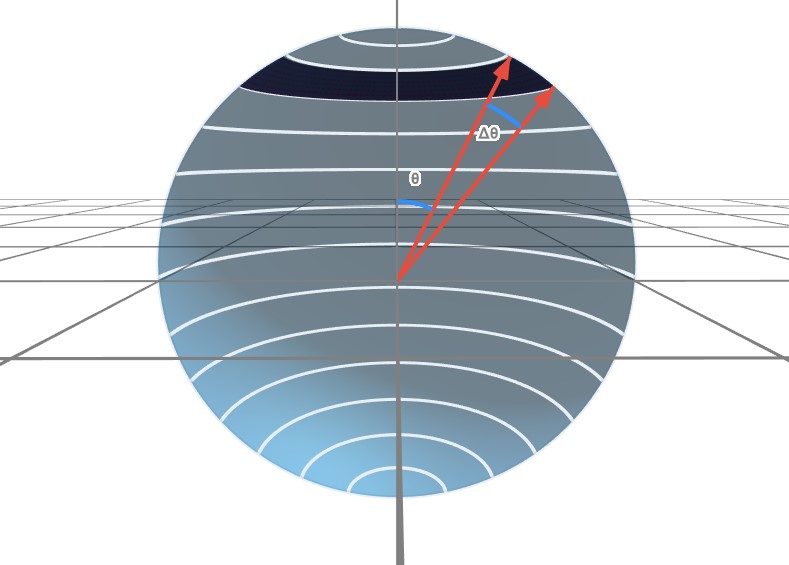
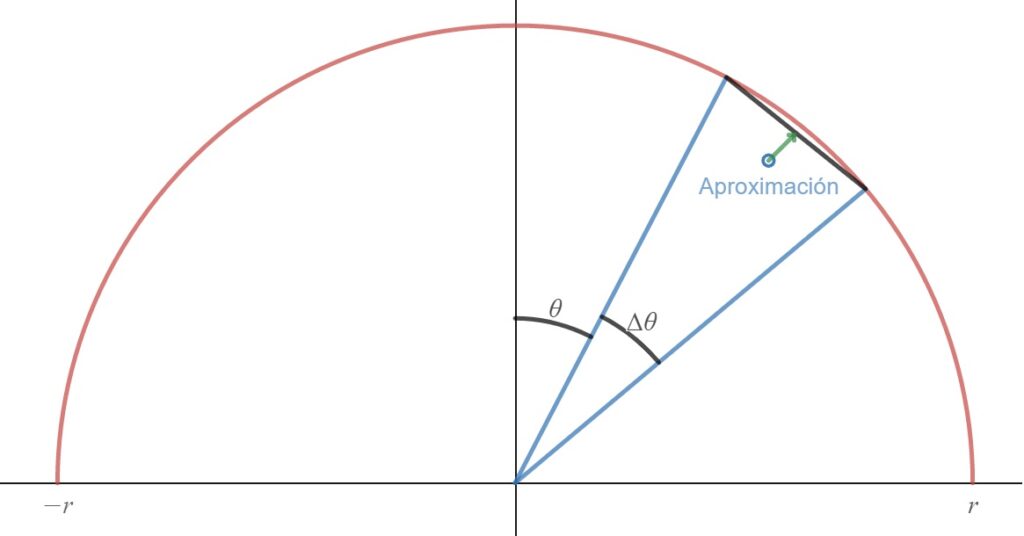
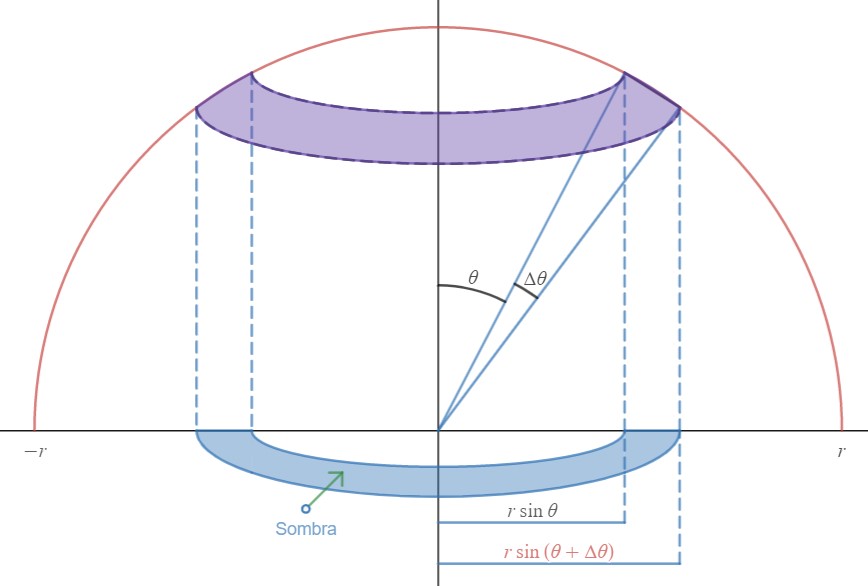
Considere una esfera de radio $r$, fijo, y realice cortes paralelos al plano $xy$, tal como se muestra en la figura 2. Entre dos cortes contiguos hay anillos circulares que identificaremos de acuerdo al ángulo $\theta$ que forman la línea que une al centro de la esfera con un punto del anillo y el eje $z$, es decir, el anillo $R_\theta$ corresponde al ángulo $\theta$ $($véase Figura 3$)$. Además, denote a la apertura angular por $\Delta\theta$. Puede ser de utilidad pensar este problema como si fuera uno de integración: mientras $\Delta\theta$ se hace más pequeño, la suma del área de la superficie de los anillos se acerca cada vez más a la superficie de la esfera. Es decir, si observa lateralmente nuestra esfera, la superficie que calcularemos como una aproximación será aquella que resulta de unir «linealmente» dos cortes contiguos. Una mejor explicación gráfica se encuentra en la figura 4.
De acuerdo, con las definiciones anteriores, se tiene que $\theta$ toma valores entre $0$ y $\pi$. Mientras que la apertura angular $\Delta\theta$ se hará más pequeña cada vez que realicemos más cortes regulares a lo largo de la superficie de la esfera y así las aproximaciones de la misma serán más precisas. Tal vez te resulte tentador interpretar la frase «$\Delta\theta$ cada vez más pequeño» como la tendencia $\Delta \theta \rightarrow 0$ de un límite adecuado; sin embargo, toda tentación por integrar o tomar límites debe ser puesta a un lado, pues el camino que tomaremos muestra de forma más evidente la relación entre la superficie y su sombra.
Pregunta 1. ¿Cuál es la circunferencia de cada anillo $($en términos de $r$ y $\theta$$)$?
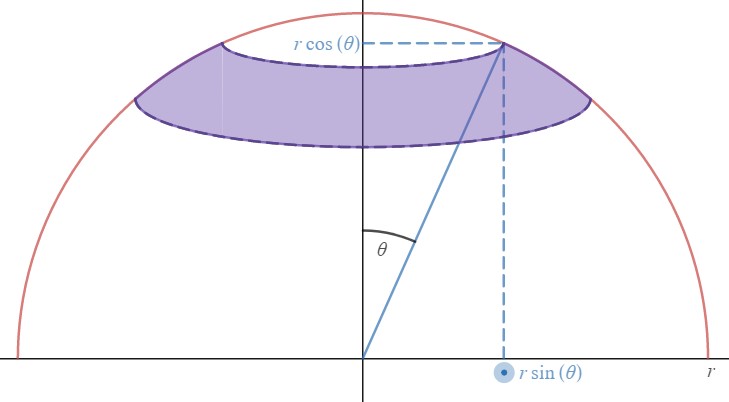
Para cada anillo $R_\theta$ calcularemos la circunferencia del anillo interno. Para ello, necesitamos encontrar el radio del anillo interno o, en otras palabras, hallar la longitud del cateto opuesto del triángulo formado por el eje $z$ y el vector director del anillo $R_\theta$ $($Figura 5$)$. Por construcción, el ángulo es $\theta$ de modo que el radio interno que buscamos es
$$r\sin(\theta).\quad (3)$$
De esta manera, la circunferencia del anillo $R_\theta$ es
$$2\pi r\sin(\theta)\quad(4)$$
Note que al multiplicar esta cantidad por $r\Delta \theta$, que es la longitud del arco generado por la apertura del anillo, obtiene una aproximación de la superficie del anillo, es decir
$$\mathcal{S}\left(R_\theta \right)= 2\pi r^2\sin(\theta)\Delta \theta.\quad (5)$$
Hasta este punto, si considera a $\Delta \theta$ como un diferencial e integramos sobre el dominio de $\theta$, obtendríamos el mágico resultado. Sin embargo, tomaremos un camino alterno para mostrar la relación que perseguimos.
En orden de conseguir esa relación, se plantea lo siguiente:
Pregunta 2. ¿Cuál es el área de la sombra sobre el plano $xy$ de uno de estos anillos $R_\theta$ $($en términos de $r$, $\theta$ y $\Delta \theta$$)$?
Recuerde que para obtener el área de un anillo bidimensional hay que encontrar el radio interno y externo que lo forman. Para esto, en la pregunta 1 ya hemos calculado el radio interno del anillo superficial, que coincide con el radio interno de la sombra del anillo. Por otro lado, note que el radio externo resulta ser la longitud del cateto opuesto del triángulo formado por el centro de la esfera y el corte externo de en la superficie de la esfera $($véase la figura 6$)$. De este modo, el área de la sombra del anillo, denotada por $A(R_\theta)$, resulta ser
\begin{align}
A\left(R_\theta\right) &= \pi r^2\sin^2(\theta+\Delta\theta) – \pi r^2 \sin^2(\theta)&&(6) \\ &= \pi r^2\left(\sin^2(\theta+\Delta\theta) – \sin^2(\theta)\right).&&(7)
\end{align}
Para la siguiente pregunta tome en cuenta que el área de cada sombra de un anillo es exactamente la mitad de la superficie aproximada $($pregunta 1$)$ de algún anillo distinto al que genera dicha sombra. Es decir:
Pregunta 3. Para la sombra de un anillo cualquiera, ¿cuál es el anillo que tiene el doble de área?
Ayuda replantear esta pregunta en otros términos: Sea $\theta_1$ fijo. Encontrar $\theta_2$ que satisfaga
\begin{equation}\label{eq:relationangles}
A\left(R_{\theta_1}\right)= \frac{1}{2}\mathcal{S}\left(R_{\theta_2}\right)\quad(8)
\end{equation}
donde $A\left(R_{\theta_1}\right)$ es el área de la sombra generada por el anillo de ángulo $\theta_1$; y $\mathcal{S}\left(R_{\theta_2}\right)$ es el área de la superficie del anillo generado por el ángulo $\theta_2$.
De la relación en (8) se obtiene que:
\begin{align}
\pi r^2\left(\sin^2\left(\theta_1+\Delta\theta\right) – \sin^2\left(\theta_1\right)\right) &= \frac{1}{2}(2\pi r^2\sin\left(\theta_2\right)\Delta\theta),&&(9)\\ \label{eq:simplification}
\iff \sin^2\left(\theta_1+\Delta\theta\right) – \sin^2\left(\theta_1\right) &= \sin\left(\theta_2\right)\Delta\theta.&&(10)
\end{align}
Si expande la suma de ángulo dentro del seno, consigue que:
\begin{align}
\sin\left(\theta_1 + \Delta\theta\right) &=\sin\left(\theta_1\right)\cos(\Delta\theta) + \sin(\Delta\theta)\cos\left(\theta_1\right),&&(11)\\
\label{eq:approximation}
&\approx \sin\left(\theta_1\right) + \cos\left(\theta_1\right)\Delta\theta.&&(12)
\end{align}
Tome en cuenta que en (12) hemos considerado las aproximaciones $\cos(\Delta\theta) \approx 1$ y $\sin(\Delta\theta)\approx\Delta\theta$, pues se ha de considerar $\Delta\theta$ pequeña. Por lo tanto, al sustituir la aproximación (12) en el lado izquierdo de (10), se tiene que
\begin{align}
\left(\sin\left(\theta_1\right)+\cos\left(\theta_1\right)\Delta\theta\right)^2-\sin^2\left(\theta_1\right) = 2\sin\left(\theta_1\right)\cos\left(\theta_1\right)\Delta\theta + \cos^2\left(\theta_1\right)(\Delta\theta)^2.\quad(13)
\end{align}
En la última expresión se puede remover el término $\cos^2\left(\theta_1\right)(\Delta\theta)^2$ pues su aportación se vuelve completamente marginal si toma una apertura de ángulo cercana a $0$. De esta manera, se obtiene la siguiente relación:
\begin{equation}
\sin\left(2\theta_1\right) = \sin\left(\theta_2\right)\quad(14)
\end{equation}
Es decir, $\theta_2 = 2\theta_1$ con la restricción $($la función seno resulta ser inyectiva cuando tiene por dominio al intervalo $[0,\pi/2]$$)$ de tomar $\theta_1\in[0,\pi/2]$ para que tengamos que $\theta_2\in[0,\pi]$.
En resumen, hemos demostrado que
\begin{equation}\label{eq:shadowandsurface}
A\left(R_{\theta}\right) = \frac{1}{2}\mathcal{S}\left(R_{2\theta}\right), \qquad \forall \theta\in\left[0,\frac{\pi}{2}\right].\quad(15)
\end{equation}
Pregunta 4. Utiliza el resultado anterior para encontrar una correspondencia entre las sombras de los anillos en el hemisferio norte de la esfera y los anillos pares, es decir, cada 2 anillos en la superficie de la misma.
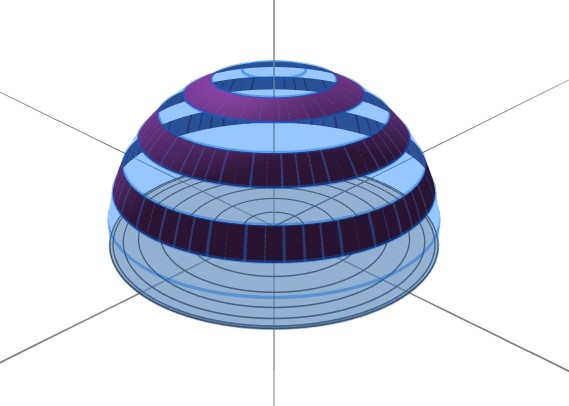
Notemos que la sombra de los anillos en el hemisferios norte generan un círculo de radio $r$. Además, cada sombra viene de un anillo cuyo ángulo es un múltiplo $($entero$)$ de la apertura angular, y gracias al resultado anterior, tenemos la siguiente relación:
\begin{equation}
A\left(R_{k(\Delta\theta)}\right) = \frac{1}{2}\mathcal{S}\left(R_{2k(\Delta\theta)}\right).\quad(16)
\end{equation}
La relación que se obtiene se interpreta como que la sombra producida por los anillos del hemisferio norte $($un círculo de radio $r$$)$ de la esfera es igual a la mitad de la suma de la superficie de los anillos pares $($uno sí y uno no$)$.
Pregunta 5. ¿Por qué lo anterior implica que el área de la sombra es la cuarta parte de la superficie?
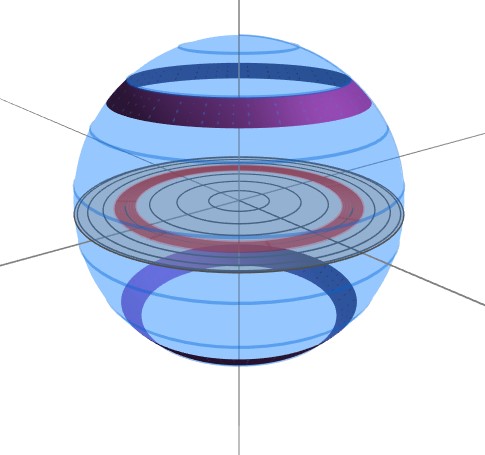
Note que el anillo superficial de ángulo $\theta$ en el hemisferio norte, tiene su simétrico en el ángulo $\pi-\theta$. Esto quiere decir que la sombra de dos anillos simétricos es cubierta por el anillo de ángulo $2\theta$. Es decir, gracias a la identidad (15) se tiene que
\begin{align}
&A\left(R_\theta\right) = S\left(R_{\pi-\theta}\right)&&(17)\\
\implies &S\left(R_\theta\right) + A\left(R_{\pi-\theta}\right) = \mathcal{S}\left(R_{2\theta}\right)&&(18)
\end{align}
Luego, la mitad de la superficie está cubierta por lo anillos pares por lo que:
\begin{equation}
\mathcal{S}\left(R_{\text{pares}}\right) = \frac{1}{2}\mathbf{SE},\quad(19)
\end{equation}
donde $\mathbf{SE}$ representa la superficie total de la esfera. Por lo tanto, debido a la relación encontrada en la pregunta 4, se tiene que:
\begin{equation}
A_{\text{sombra}} = \frac{1}{2} \mathcal{S}\left(R_{\text{pares}}\right) = \frac{1}{4}\mathbf{SE},\quad(20)
\end{equation}
donde $A_{\text{sombra}}$ representa el área de la sombra de la esfera. Finalmente, como la sombra es un círculo de radio $r$, el área de la sombra es $\pi r^2$, por lo que:
\begin{equation}
\mathbf{SE}=4\pi r^2.\qquad\blacksquare\quad(21)
\end{equation}
3blue1brown
La idea de los pasos seguidos en la prueba anterior se basan en un vídeo interactivo [1] del canal 3blue1brown en el que se guía la demostración en forma de preguntas, pero sin dar la respuesta a ellas. A este tipo de resolución de problemas se les conoce como ejercicios guiados.
Dentro de la inmensidad de canales en Youtube con contenido matemático se encuentran Julioprofe, Numberphile, Derivando, entro otros. Uno de ellos, creado por Grant Sanderson, 3blue1brown $($Figura 9$)$ es un canal que, en palabras de su creador, es una combinación de matemáticas y entretenimiento. El propósito de dicho canal es explicar problemas difíciles dentro de la matemática mediante animaciones y bajo simple cambios de perspectiva. En opinión de los autores que redactan estas líneas, los vídeos mantienen esa creatividad y curiosidad de la que se habló en párrafos anteriores.
En este canal podrán encontrar de todo, desde matemáticas recreativas, como la solución a las torres de Hanoi, hasta visualizaciones de conceptos más prácticos dentro de la matemática aplicada, tales como la simulación de una epidemia, aproximaciones mediante series de Fourier; o también soluciones a problemas de olimpiadas matemáticas. En fin, la única limitante de los vídeos de este canal es su propia naturaleza de ser finitos. Invitamos a los lectores a que se maravillen del basto contenido ofrecido por este canal y que, de paso, interactúen con algunas otras plataformas dedicadas a la divulgación de contenido matemático de forma accesible pero con el suficiente rigor.
Conclusiones
En una clase de matemáticas es común que los ejercicios vistos en clase sirvan como base para las tareas o los exámenes, ya sean en el resultado mismo o en el procedimiento. Esto puede impulsar en el joven estudiante la idea de que las demostraciones solo son útiles en tanto pueden contribuir a un resultado más grande. Evidencia suficiente para esta aseveración se puede encontrar en la famosa frase «¿Y esto va a venir en el examen?» y la inmediata pérdida de interés en más de una persona cuando la respuesta es negativa.
En cierto sentido, este fenómeno es tan solo un eco distante de la arbitrariedad que discutíamos al principio de este artículo. Si una demostración no tiene valor en sí misma, entonces tan solo es otra herramienta arbitraria más destinada a usarse para otro propósito desconocido aún más grande. Y bajo este razonamiento podríamos haber navegado cien leguas en el mar infinito del conocimiento y aún así sentir que no llegamos a ningún lado.
Combatir y aplacar la arbitrariedad es entender la belleza de los resultados tan solo por lo que significan, y no solo por lo que nos pueden traer más adelante. Es redescubrir la fórmula del área superficial de una esfera tan solo por querer hacer evidente la relación con su sombra. En el gran mar del conocimiento este no es un resultado que no conociéramos antes, mas el valor de la prueba no está en la fórmula, sino en su capacidad de satisfacer la curiosidad. Porque la curiosidad, tan personal como es, es uno de los mejores motivadores que existen; es nuestra propia linterna que nos guía en nuestra travesía por el mar infinito que son las matemáticas.
Y para aquellos que encuentran su pasión en la parte «aplicada», de Matemáticas Aplicadas, esa linterna es aún más importante pues surcarán más de un solo mar en su travesía. Las matemáticas son tan nobles que encajan en cualquier campo: computación, economía, estadística, química, lógica, inteligencia artificial, medicina, hasta dentro de la filosofía se encuentran los primeros fundamentos lógicos. Puro o aplicado, es fácil reconocer a quien disfruta y ama esta ciencia exacta con tan mala reputación. Basta con encender una chispa de curiosidad frente a sus ojos. Esa cuestión no lo abandonará hasta haberla saciado y, con suerte, en el camino habrá encendido otras tantas llamaradas por si mismo.
Así como el profesor Guillermo Grabinsky dijo una vez [2]:
«Amen las matemáticas, hagan matemáticas lo mejor que puedan, disfruten las matemáticas, déjense deslumbrar. […] Yo sigo deslumbrado.»
Referencias
[1] 2blue1brown. But why is a sphere’s surface area four times its shadow?. Dic 2018. Disponible en este link https://www.youtube.com/watch?v=GNcFjFmqEc8.
[2] Mesa redonda: Matemáticas puras vs aplicadas, Sep 2019.Disponible en este link https://web.facebook.com/watch/live/?v=498676644027547ref=watch_permalink.
Software
Las imágenes del presente texto fueron creadas en desmos.com y math3d.org.
