Formulación bayesiana de procesos Gaussianos

Alfredo Garduño Iñigo
Director de la Maestría en Ciencia de Datos

El aprendizaje automático $($machine learning$)$ se ha filtrado en la mayoría de los campos científicos. Una de las ideas que más se utilizan es el poder encontrar una función a partir de un conjunto de valores que determinan ciertas propiedades de un proceso $($entradas$)$ y el resultado de este proceso bajo dicha configuración $($salidas$)$. Desde el punto de vista de una experta en aprendizaje de máquina esto se puede resolver bajo el esquema de aprendizaje supervisado. Para una experta en estadística, esto se resuelve con la formulación de un problema de regresión. Para una matemática, esto se resuelve encontrando la superficie de respuesta entre la configuración. Si cada una revisa la literatura de su campo encontrará varios modelos candidatos y, posiblemente, si hablan entre las tres, encontrarán en la intersección el mismo modelo bajo distintos nombres, motivaciones y propiedades estudiadas. Nos referimos a un proceso Gaussiano.

El proceso Gaussiano es uno de esos modelos que ha estado presente en la literatura de diversas áreas como ciencias de la tierra [1], ingeniería [5] y aprendizaje automático [9], por mencionar algunas. Dependiendo del origen de la aplicación se han estudiado sus propiedades y su formulación desde distintos ojos. Es uno de los pocos modelos que se ha estudiado y del cual se conocen bastantes garantías teóricas. Sin duda, son útiles y aún cuando son modelos computacionalmente costosos, se sigue desarrollando teoría que permite moldearlos a aplicaciones en la frontera del conocimiento.

La idea de escribir esta entrada viene de leer la nota de [10] y de la intención del autor de divulgar el uso de uno de los modelos más flexibles en la literatura. En este artículo nos centramos en su motivación como un modelo de regresión planteado desde una formulación bayesiana. Puesto que permite construir un modelo de inferencia para objetos de dimensión infinita $($funciones$)$ en lugar de la tradicional aplicación de objetos de dimensión finita $($vectores$)$. Por supuesto, esta formulación tiene deficiencias en cuanto el entendimiento de un proceso Gaussiano como un proceso estocástico o la mejor aproximación en un espacio funcional particular. Pero dejaremos esto para subsecuentes entradas si es que hay interés.

El proceso Gaussiano surge en estudios de minería al desarrollar un modelo para predecir la concentración de pepitas de oro en un espacio de 2 dimensiones [6]. La idea es sencilla, se tienen ciertas ubicaciones donde se han realizado excavaciones y se tiene el registro de la producción de dichas localidades. Para predecir la producción en lugares no explorados basamos nuestra formulación en buscar la mejor combinación lineal de los datos bajo un esquema de dependencia geográfica. Esta dependencia geográfica es un mecanismo para incorporar cercanía en las predicciones basada en la cercanía de las localidades.

El modelo resultante es denominado como Kriging y es uno de los modelos más utilizados en aplicaciones de geoestadística [7] y el precursor de lo que ahora llamamos procesos Gaussianos en el área de aprendizaje de máquina [9].

En general, un proceso Gaussiano nos permite modelar una función $f: X\to Y$ donde $X\subset \mathbb R^p$ es el espacio configuraciones $($inputs$)$ y $Y\subset \mathbb R^d$ el espacio de respuestas (outputs). La idea es sencilla. Supongamos que tenemos una colección de pares $D =\left\lbrace(x_i,y_i)\right\rbrace_{i=1}^n$ donde

$$y_i=f(x_i)$$,

donde por conveniencia asumiremos $d=1$. Es decir, la salida de $f$ es un escalar [¹]. Describiremos nuestro candidato $h: X\to Y$ como una función que sea capaz de predecir exactamente $h(x_i) = y_i$ para cualquier par en $D$ y, además, que la respuesta sea suficientemente buena $h(x^\ast ) \approx f(x^\ast )$ para $x^\ast \in X\D$. Una función con estas propiedades se denomina interpolador. Sin embargo, el supuesto Eq. $($1$)$ en distintas aplicaciones no es suficientemente realista.

Incluso en aplicaciones donde $f$ es la salida de un código computacional éste puede estar sujeto a variaciones inherentes al proceso que se está computando. Por ejemplo, en aplicaciones climáticas [3] el modelo computacional son promedios temporales de procesos atmosféricos $($sistemas caóticos con un conjunto atractor$)$[²] sujetos a variabilidad temporal y a incertidumbre en valores iniciales. Esto es porque $f$ representa la resolución de un sistema de ecuaciones que buscan equilibrios energéticos. En la analogía de minería esto representaría una variabilidad no reducible sujeta a la detección de pepitas de oro hasta cierta escala volumétrica.

Esto nos lleva a suponer una respuesta del estilo

$$y_i=f(x_i)+\varepsilon_i$$

donde $\varepsilon$ denota la variabilidad estocástica de la respuesta. Usualmente este término es modelado como una variable aleatoria con media $0$ y varianza $\sigma_{\varepsilon^2}$. Bajo este esquema el modelo $h$ pierde su propiedad de interpolación pero esperamos poder regularizarlo de tal forma que nuestro modelo sea un \textbf{suavizador} de la respuesta de la función $f$.

De lo anterior sabemos lo siguiente: buscamos en $h$ una función que podemos usar como sustituto de $f$. Es decir, debemos de poder evaluar en cualquier punto donde $f$ esté definida. Además, en $h$ podemos incorporar la variabilidad que esperaríamos incluso en las configuraciones que ya hemos evaluado.

FORMULACIÓN BAYESIANA

La incorporación de distintos factores sobre los que podemos hacer inferencia presenta oportunidades para realizar de manera sistemática cuantificación de incertidumbre en distintos componentes de nuestro modelo. La forma de operar esto es bajo un esquema bayesiano de actualización de incertidumbre [1]. Lo que exploraremos a continuación sigue la formulación típica desde el punto de vista de una experta en aprendizaje automático con un toque de formulación bayesiana para un proceso Gaussiano.

Un proceso Gaussiano está definido por medio de la distribución conjunta

$$h \sim N(\mu,\Sigma)$$,

donde $h,\mu \in \mathbb R^n$ denotan los vectores con entradas $h_i = h(x_i), \mu i = \mu (xi)$, y $\Sigma \in \mathbb R^{nxn}$ denota la matriz de covarianzas con entradas $\Sigma {ij} = c(x_i,x_j)$ para alguna función positiva definida $c(\cdot ,\cdot )$ a la cual nos referimos como kernel y permite la definición válida de una matriz de covarianzas. Esto nos permite construir la distribución conjunta de evaluaciones finitas de la función $h$ para cualquier conjunto $x_1, . . . , x_n$ de tamaño arbitrario $n$. Es decir, cualquier $n$ y cualquier conjunto de evaluaciones $x_i$ nos permitirá definir una distribución conjunta Gaussiana si tenemos en nuestro conocimiento una función media y una función kernel. Ahora, la función kernel debe ser una función positiva definida para poder definir una matriz válida de covarianzas para lo cual tenemos la siguiente definición.

Definición. Una función positiva definida es aquella que para cualquier entero $N$, colección de puntos $x_1, . . . , x_N$ , y cualquier conjunto de coeficientes $α_1, . . . , α_N$ no todos iguales a cero, satisface

$$\sum_{j=1}^{N}\sum_{k=1}^{N} \sigma _j \sigma_k c(x_j,x_k) \geq 0$$

Por otro lado, es común utilizar una función $\mu (x) = g(x)^T\Beta$ (pensemos en un modelo de regresión tradicional) donde $g(\cdot)$ puede estar compuesto por distintas potencias, productos cruzados, u otro tipo de transformaciones de los datos de entrada. Si se tiene conocimiento previo sobre la función f esta es una formulación bastante útil y se pueden incorporar distintos términos al mismo estilo que un modelo de regresión aditivo [11]. Sin embargo, es usual considerar $\mu (\cdot) = 0$ $($en especial en aplicaciones de aprendizaje automático$)$ y dejar toda la carga de inferencia sobre la función kernel.

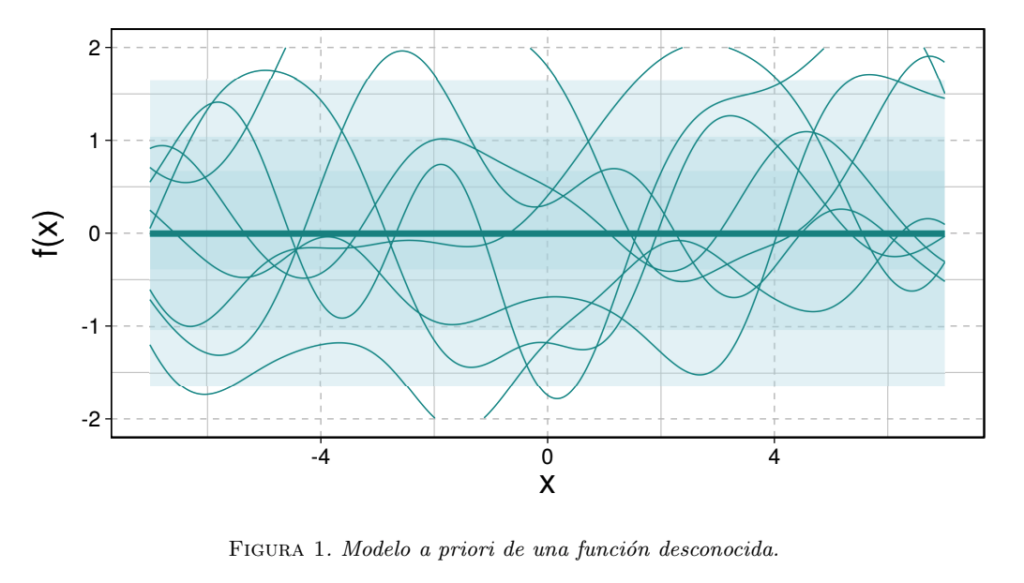
Ahora, supongamos $\mu = 0$ y que el ruido observacional en la Eq. $($2$)$ lo podemos modelar como una variable aleatoria Gaussiana. El modelo en la Eq. $($3$)$ se interpreta como una distribución previa y la ilustramos en la Fig. 1 donde podemos ver la función media $($la línea horizontal$)$, y distintas realizaciones aleatorias de una función bajo este modelo previo. Por otro lado, tenemos que para cualquier conjunto de observaciones nuevas $($ejercicio típico siguiendo la regla de actualización de Bayes para vectores aleatorios Gaussianos$)$ se satisface [³]

$$h_\ast|D \sim N(k_{\ast}^T[\Sigma + \sigma {\varepsilon}^2]y,\Sigma{\ast}-k_{\ast}[\Sigma+\sigma_{\varepsilon}^2]k_{\ast}^T)$$

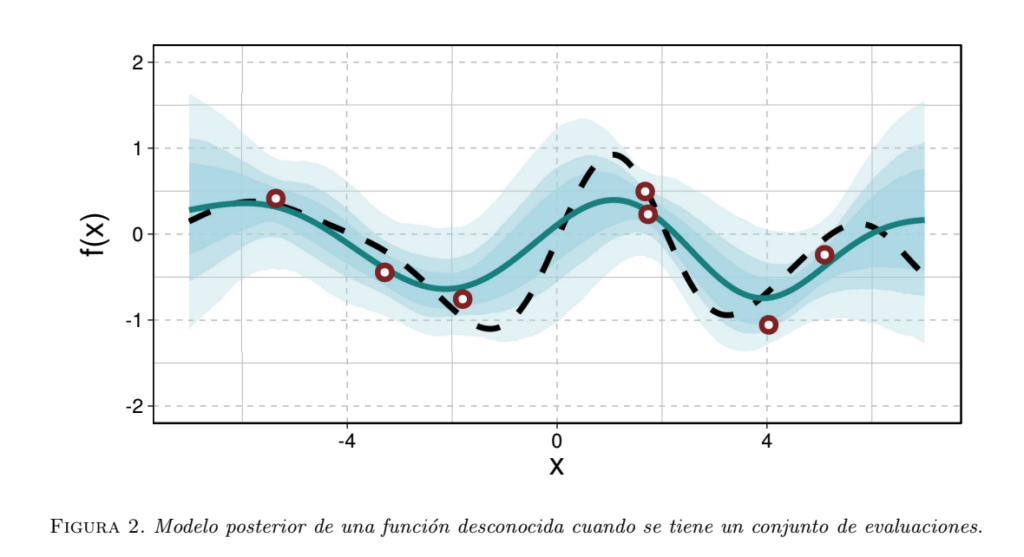
donde $h_\ast \in \mathbb R^m$ y cada componente es la predicción de $f$ en una ubicación nueva $x_{\ast}^1, . . . , x_{\ast}^m$ que no se encuentra en $D; k_{\ast} \in \mathbb R^{n\times m}$, resulta de evaluar la función \textit{kernel} en cada posible pareja cruzada (es decir, $x_j$ y $x_{\ast}^k$ para todo par de índices $j = 1, . . . , n$ y $k = 1, . . . , m$); y $\Sigma \ast \in \mathbb R^{m\times m}$, es la matriz de covarianzas evaluada en todas las parejas de configuraciones no observadas $(x{\ast}^1, . . . , x_{\ast}^m)$. Esto lo podemos ver en la Fig. 2 donde la función posterior se ha actualizado de acuerdo a las evaluaciones que tenemos de la función que estamos ajustando.

Observaciones

• La regla de actualización bayesiana opera bajo objetos de dimensión finita $($vectores$)$ aún cuando $h$ es una función que suponemos vive en un espacio de funciones $($que suponemos es un espacio de Hilbert$)$.
• La regla de actualización ilustra que el supuesto de $h$ bajo un proceso Gaussiano refleja nuestras creencias previas $($a priori$)$ sobre $h$ como una función. Es decir, codificamos ciertas propiedades a través de la función media y la función kernel.
• La función kernel está completamente especificada en la Eq. $($5$)$. Es decir, la regla de actualización no actualiza parámetros de c. Para esto último, necesitamos definir un modelo generativo $($jerárquico$)$ en el kernel.
• La función kernel nos ayuda a definir propiedades promedio de la función $h$ como continuidad, diferenciabilidad, etc.

La pregunta natural sobre este modelo es sobre la función kernel $c$. ¿Qué funciones son compatibles? ¿Bajo qué funciones kernel se incorporan supuestos particulares de continuidad y diferenciabilidad?

La regla de actualización y la estructura Gaussiana limitan la colección de funciones kernel que pueden ser consideradas. Y es por esto que muchas veces nos limitamos a escogerlas de un catálogo muy particular de funciones posibles. El teorema de representación de Mercer nos permite caracterizar una función kernel en términos de su representación espectral $($valores y funciones propios$)$ [⁴]. Adicionalmente, las funciones kernel satisfacen ciertas propiedades algebraicas (suma y multiplicación) lo cual nos permite extender dicho catálogo a cuestiones mas generales $($ver el capítulo 4 de [9]$)$.

El lector perspicaz seguro ha identificado que para construir una función aleatoria lo hemos hecho a partir de considerar vectores aleatorios de dimensión variable pero finita. Por supuesto, en esta construcción hemos ocultado debajo del tapete el teorema de extensión de Kolmogorov que nos permite caracterizar la ley de probabilidad de un proceso aleatorio por medio de la distribución conjunta de una colección de finita de variables aleatorias $($Procesos Estocásticos I$)$. Adicionalmente, hemos utilizado un abuso de lenguaje que hemos heredado de autores en aprendizaje de máquina como en [9], donde estrictamente hablando un proceso Gaussiano debería de ser llamado \textbf{campo Gaussiano}. Esto último pues un campo aleatorio esta definido para una colección de variables aleatorias indexadas por un conjunto de dimensión mayor a uno [1]. En contraparte, un proceso estocástico está indexado por una variable de una dimensión como el tiempo [⁵].

Por supuesto, esta discusión nos lleva a considerar la definición del espacio donde definimos nuestros eventos de probabilidad $($la $\sigma$- álgebra necesaria$)$ [⁶] pues esto es necesario cuando operamos con un proceso Gaussiano en condiciones más exóticas que una regresión. Por ejemplo, cuando nos interesa obtener promedios $($integrales$)$ de la salida de un proceso Gaussiano, o cuando nos interesa modelar la logverosimilitud de un proceso computacionalmente costoso $($como en problemas inversos bayesianos [4]$)$ es necesario tener una correcta caracterización del modelo para garantizar que no haya sorpresas matemáticas.

Conclusión

El uso de los procesos Gaussianos es casi universal y en áreas como aprendizaje de máquina es una de las pocas alternativas para modelar respuestas no lineales. Para explotar su aplicación en distintos problemas usualmente se requiere de una aproximación para ser computacionalmente factibles. Esto ha generado interés para estudiar sus propiedades límite $($consistencia$)$ y las conexiones que presentan como procesos estocásticos a otro tipo de objetos matemáticos como ecuaciones diferenciales estocásticas [8].

Dejaremos para siguientes entradas la formulación bajo una medida de probabilidad en espacios arbitrarios, una de las intersecciones más interesantes entre análisis funcional y probabilidad. Esto último representa uno de los quehaceres más interesantes de un matemático aplicado.

Pues un mismo objeto o modelo puede ser estudiado bajo distintos puntos de vista y explotar todas sus propiedades. El área de cuantificación de incertidumbre, el área principal de investigación de este autor, es un área que presenta estas ventajas y bellos pasajes de la matemática, probabilidad y estadística. Si estás interesado en explorar estas conexiones en tu proyecto de tesis puedes contactarme con muchísimo gusto.

1. La extensión multivariada representa un tema interesante para explorar en una tesis de licenciatura de matemáticas aplicadas, actuaría o ciencia de datos. ↩︎
2. Sistemas dinámicos II. ↩︎
3. Cálculo de probabilidades II. ↩︎
4. Álgebra Lineal. ↩︎
5. Esto realmente no lo había identificado sino hasta leer [10], que sirvió como base para escribir esta entrada. ↩︎
6. Teoría de la Medida. ↩︎

Referencias

1. R. J. Adler. The Geometry of Random Fields. Society for Industrial and Applied Mathematics, Philadelphia, siam edition, 2010. ISBN 978-0-89871-693-1. 1, 5
2. J. M. Bernardo and A. F. M. Smith. Bayesian Theory. Wiley Series in Probability and Statistics, 2001. 2
3. E. Cleary, A. Garbuno-Inigo, S. Lan, T. Schneider, and A. M. Stuart. Calibrate, emulate, sample. Journal of Computational Physics, 424:109716, Jan. 2021. ISSN 00219991. 2
4. M. Dashti and A. M. Stuart. The Bayesian Approach to Inverse Problems. In R. Ghanem, D. Higdon, and H. Owhadi, editors, Handbook of Uncertainty Quantification, pages 311–428. Springer International Publishing, Cham, 2017. ISBN 978-3-319-12384-4 978-3-319-12385-1. 5
5. A. I. J. Forrester, A. Sóbester, and A. J. Keane. Engineering Design via Surrogate Modelling:A Practical Guide. Wiley, first edition, July 2008. ISBN 978-0-470-06068-1 978-0-470-77080-1.1
6. D. G. Krige. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Southern African Institute of Mining and Metallurgy, 52(6):119–139, 1951. 1
7. C. Lantuéjoul. Geostatistical Simulation. Springer Berlin Heidelberg, Berlin, Heidelberg, 2002. ISBN 978-3-642-07582-7 978-3-662-04808-5. 2
8. F. Lindgren, D. Bolin, and H. Rue. The SPDE approach for Gaussian and non-Gaussian fields: 10 years and still running. arXiv:2111.01084 [stat], Nov. 2021. 6
9. C. E. Rasmussen and C. K. I. Williams. Gaussian Processes for Machine Learning. Adaptive Computation and Machine Learning. MIT Press, Cambridge, Mass, 2006. ISBN 978-0-262-18253-9.1,2,5
10. D. Simpson. Yes but what is a Gaussian process? or, Once, twice, three times a definition; or A descent into madness. https://dansblog.netlify.app/posts/2021-11-03-yes-but-what-is-a-gaussian\\-process-or-once-twice-three-times-a-definition-or-a-descent-into-madnes1
11. S. N. Wood. Generalized Additive Models. CRC Press, 2017