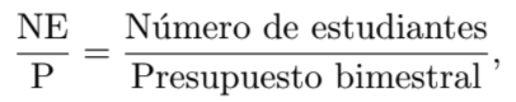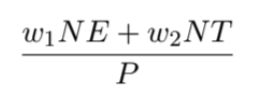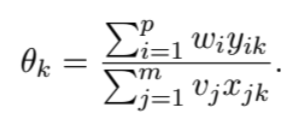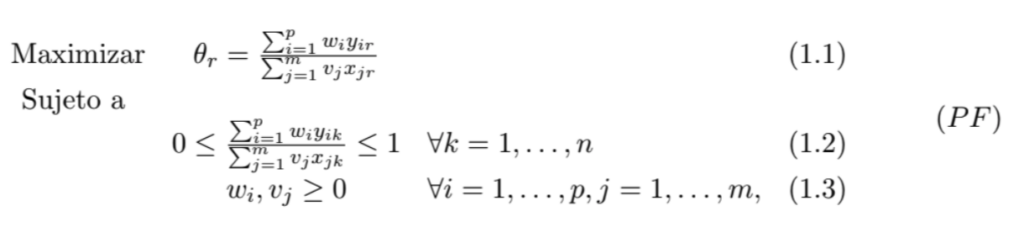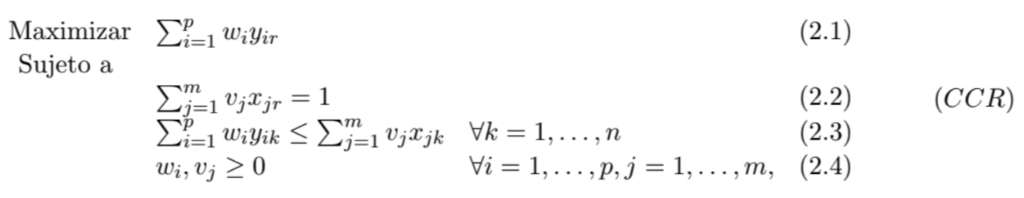¿Quién lo hizo mejor?

o de la eficiencia usando análisis envolvente de datos

Edgar Possani Espinosa

Profesor de tiempo completo

¿En qué pensamos cuándo queremos comparar el desempeño o la eficiencia? Si pensamos en fútbol y queremos comparar a jugadores delanteros podemos pensar en la fracción:

Número de goles / Número de partidos jugados

si pensamos en la eficiencia energética de un automóvil podemos pensar en:

Kilómetros recorridos / Litos de gasolina

el análisis envolvente de datos $($AED$)$ [1] es un área de la optimización matemática que se preocupa por contestar qué es la eficiencia, y cómo medirla. Uno de los primeros artículos académicos $($Ver Figura 1$)$ sobre el tema lo escribieron Charnes, Cooper y Rhodes [2] en 1978¹, su interés inicial era el de poder evaluar el desempeño de escuelas en Estados Unidos.

Midiendo a las mejores escuelas

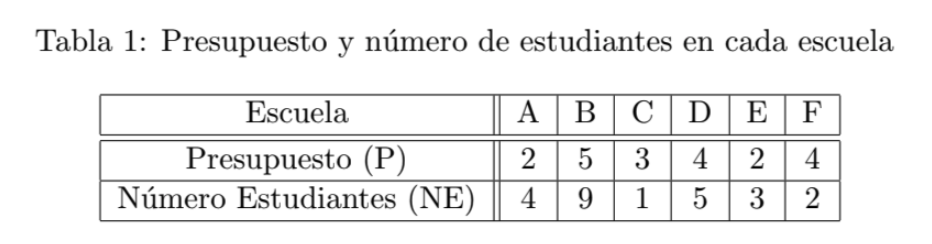
Como ejemplo consideremos los datos que se muestran en la Tabla 1. Donde se considera a 6 escuelas con su presupuesto bimestral $($en cientos de miles de pesos$)$ y número de estudiantes $($en cientos$)$.

Si proponemos como medida de eficiencia la fracción:

tendríamos como resultado las medidas que se muestran en la Tabla 2. Bajo esta medida

diríamos que la escuela $A$ $($con una eficiencia de $2.0)$ es la más eficiente y la escuela $B$ $($con una eficiencia de $1.80)$ sería la segunda mejor. ¿Qué tan más eficiente es la escuela $A$ que la $B$? La diferencia entre la eficiencia de $A$ y la $B$ es $0.2$ que es un $10\% $ de la escuela $A$. De hecho, podríamos definir a la eficiencia relativa como:

La eficiencia relativa para este ejemplo se muestra en la Tabla 3. Podríamos quizás afirmar que la escuela $A$ es $100 \%$ eficiente, la $B$ un $90 \%$ , mientras que la escuela $E$ sería un $75 \%$ eficiente en comparación con la $A$. Si en un futuro consideramos una nueva escuela, digamos una escuela $G$, con $800$ estudiantes para que esta fuese tan eficiente como la $A$ debería hacer uso de un presupuesto bimestral de $400,000$ pesos. Podemos representar esta

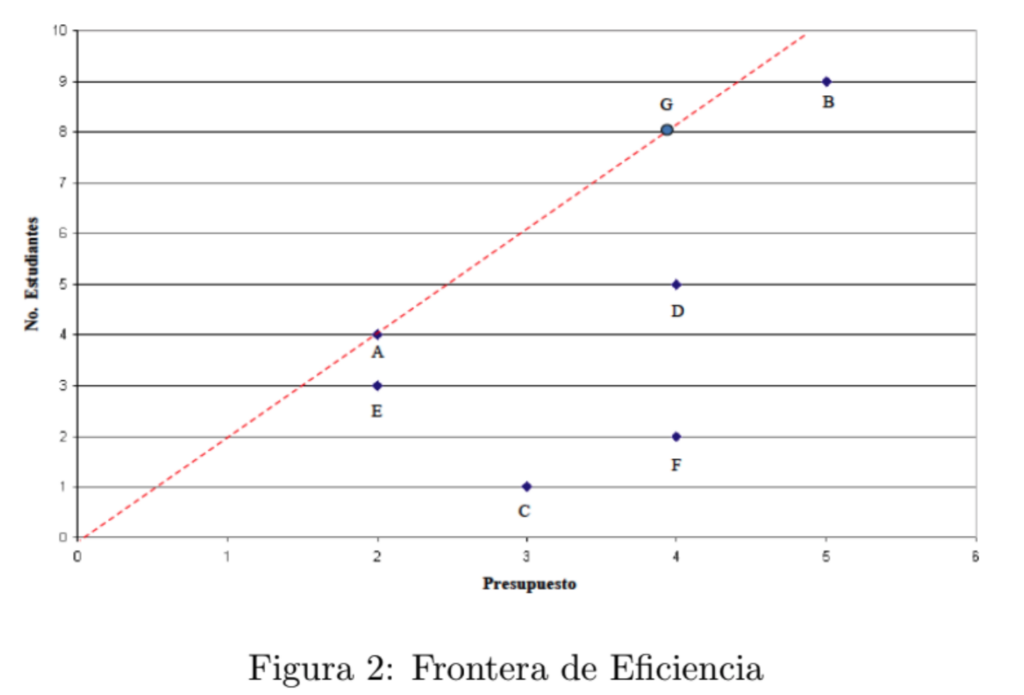
situación mediante una gráfica como la mostrada en la Figura 2. Donde el eje horizontal mide el presupuesto y el vertical el número de estudiantes, la linea punteada nos indica la frontera de eficiencia, que representa aquellas escuelas que tienen una eficiencia del $100 \%$. Como se puede ver la única escuela eficiente al $100 \%$ en los datos de la Tabla 1 es la escuela $A$, y si la nueva escuela $G$ efectivamente tiene un presupuesto de $400,000$ pesos y atiende a $800$ estudiantes entonces también estaría sobre la misma frontera como se muestra en la Figura 2.

La eficiencia la podemos considerar en diferentes contextos y se suele hablar de la función producción como aquella función que relaciona $($o devuelve$)$ algunas salidas $($en inglés outputs$)$ al recibir algunas entradas $($en inglés inputs$)$, para definir a la eficiencia en general
como la fracción:

Salidas / Entradas

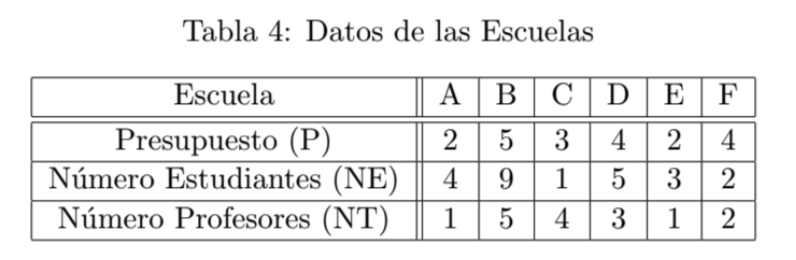
En el ejemplo anterior sólo estamos considerando como salida al “número de estudiantes” y como única entrada al “presupuesto”, en los ejemplos de principio de este texto consideramos para la eficiencia de los delanteros como salida el “número de goles” y como entrada el “número de partidos jugados”. Pero, ¿qué pasa si tenemos más de una salida? Pensemos ahora, por ejemplo, que además de tener datos sobre el número de estudiantes tenemos también el número de profesores en cada escuela $($en decenas$)$ como se muestra en la Tabla 4. Si consideramos a este dato como una salida para la función de producción

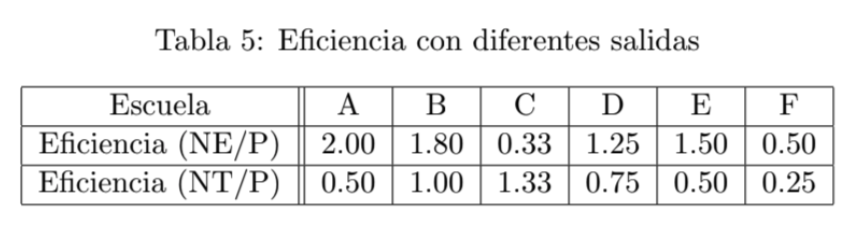
de una escuela, podríamos considerar una medida de eficiencia que sólo considere a los estudiantes $\frac{NE}{P}$ y otra que solo considere a los profesores $\frac{NT}{P}$, de dónde tendríamos la situación mostrada en la Tabla 5. En este caso bajo la eficiencia $\frac{NE}{P} $ la escuela $A$ es la

más eficiente, pero bajo la eficiencia $\frac{NT}{P}$ ahora resulta que la escuela $C$ es la más eficiente. Sin embargo, aún más interesante, podríamos intentar usar todos lo datos disponibles al mismo tiempo, para obtener una sola medida de eficiencia. Consideremos una importancia relativa $w_1$ para la salida “numero de estudiantes” y una importancia relativa $w_2$ para la salida “numero de profesores” para tomar como medida de eficiencia a la fracción:

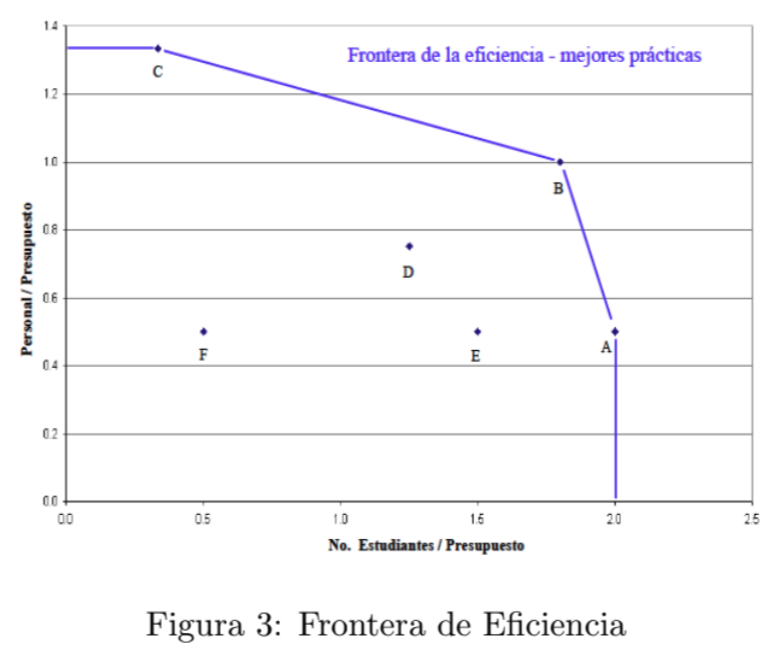
Si escogemos $w_1 = 1$ y $w_2 = 0$ entonces sólo le estaríamos dando importancia la número de estudiantes, mientras que si $w_1 = 0$ y $w_2 = 1$ sólo le estaríamos dando importancia al número de profesores. Veamos la gráfica de la Figura 3 donde el eje horizontal mide $\frac{NE}{P}$ y el eje vertical $\frac{NT}{P}$. Consideremos una envolvente² convexa que contiene a todos las escuelas en este espacio, y pensemos en la frontera de la envolvente $($la línea que une a los puntos extremos$)$ como la frontera de la eficiencia $($la que contiene a las escuelas más eficientes$)$. Bajo esta perspectiva, no solo la escuela $A$ y $C$ serían $100 \%$ eficientes sino también la escuela $B$. Aquí le estamos dando oportunidad a la escuela $B$ a ser considerada como de las más eficientes o que demuestra tener de las “mejores prácticas” ya que para su nivel de presupuesto logra dar una combinación de salidas que no es superada por ninguna otra escuela. No tiene el mejor desempeño individual en términos de alumnos $($como $A)$ o de profesores $($como $C)$ pero si en una combinación de ambas salidas.

Esta fue la práctica idea que tuvieron Charnes, Cooper y Rhodes [2] en su modelo consideran para cada escuela $k$ un vector con los datos de las salida $(y_{1k}, y_{2k}, . . . , y_{pk})$, y un vector de datos de entradas $(x_{1k}, x_{2k}, . . . , x_{mk})$ con $k = 1, . . . , n$. Notemos que se están considerando $p$ posibles salidas y $m$ posibles entradas, y $n$ diferentes escuelas (que ellos llaman unidades de decisión). Si se considera una variable que mide la importancia $w_i$ para el dato de salida $i$ y una variable que mide la importancia $v_j$ para el dato de entrada $j(\forall i = 1, . . . , p, \forall j = 1, . . . , m)$ , se puede calcular la eficiencia de la escuela $k$ bajo esas medidas de importancia como:

Pensemos que queremos ser los más “justos” o “democráticos” posibles, o al menos evitar quejas por parte de los directores de las escuelas sobre la importancia específica que se le dé a $w_i$ o $v_j$ . Así que le dejamos a cada escuela escoger los valores de $w_i$ y $v_i$ de tal suerte que su eficiencia sea la más alta posible, entonces lo único que faltaría pedir es que todas las unidades de decisión $($escuelas$)$ tengan una eficiencia entre $0$ y $1$. Así podemos plantear el problema de encontrar los mejores valores de importancia $w_i$, $v_j$ para la escuela $r$ como el problema de optimización:

Notemos que la función objetivo escrita en la ecuación $($1.1$)$ es justo la eficiencia de la escuela $r$ y se está pidiendo encontrar su valor máximo. Mientras que la ecuación $($1.2$)$ pide que las eficiencias de todas las escuelas estén entre $0$ y $1$. Por último, las ecuaciones $($1.3$)$ indican que las variables a las que hay que encontrar sus valores óptimos son $w_i$ y $v_j$ , y se están pidiendo sean positivos.

Al resolver este problema para cada escuela $r(r = 1, . . . , n)$ aquellas escuelas cuya eficiencia de $\theta_r = 1$ serían ($100 \%$) eficientes, además los valores óptimos de $w_i$ y $v_j$ podrían servirnos para saber qué entradas y qué salidas son más importantes para esa escuela, o cuáles no le ayudan a obtener una alta eficiencia $($aquellos con valores de $w_i$ y $v_i$ cercanos a cero$)$.

Resolviendo problemas de análisis envolvente de datos

La programación lineal $($ver el libro [3]$)$ es un área de las matemáticas que se dedica a resolver problemas cuya función objetivo es lineal y sus restricciones son también ecuaciones o desigualdades lineales. Este tipo de problemas se pueden resolver en tiempos computacionales razonables, y existen muchos paquetes que nos permiten encontrar sus soluciones óptimas $($ver [4].$)$ Así que Charnes, Cooper y Rhodes tuvieron la útil idea de transformar el problema $(PF)$ en un problema de programación lineal de la siguiente manera:

Notemos ahora que tanto la función como objetivo $(2.1)$, como las restricciones y desigualdades $(2.1)$-$(2.4)$ son lineales. En el artículo [5] se demuestra que los problemas $(FP)$ y $(CCR)$ son equivalentes. De hecho es fácil ver que la ecuación $(2.1)$ sólo involucra al numerador de la ecuación $(1.1)$ para $\theta_r$ y que el denominador aparece como restricción en la ecuación $(2.2)$. Por otro lado la ecuación $(2.3)$ es muy parecida ala ecuación $(1.2)$, y se puede pensar que viene de multiplicar por el término $\Sigma_{j=1}^m v_j x_{jk}$ ambos lados de la desigualdad. Existe paquetes de libre acceso que ya resuelven de manera automática para todas las unidades de decisión el problema $(CCR)$, por ejemplo se puede usar [6].

Si resulta que para una unidad de decisión $r$ al resolver $(CCR)$ tiene una eficiencia $\theta_r < 1$ esta unidad se dice es ineficiente, porque aunque esté eligiendo de la mejor manera los valores de $w_i$ y $v_j$ no llega a tener un valor de $1$ $($no llega a la eficiencia del $100 \%)$. Sin embargo, es fácil detectar qué unidades si tienen eficiencia al $100 \%$ para esos pesos optimizados de la unidad $r$, al identificar qué unidades $k$ cumplen la restricción $(2.3)$ con igualdad. A estas unidades se les suele llamar unidades de referencia, porque pueden servir de ejemplo $($o referencia$)$ en su uso de las entradas o salidas en comparación de lo que hizo la unidad $r$. Existen otras formulaciones similares y en la literatura del área hay otras conclusiones e interpretaciones económicas que se pueden sacar del análisis de las mismas. Sugiero leer los capítulos $3$ y $5$ de [1] para una buena introducción a estas interpretaciones.

Sobre las aplicaciones y otros estudios

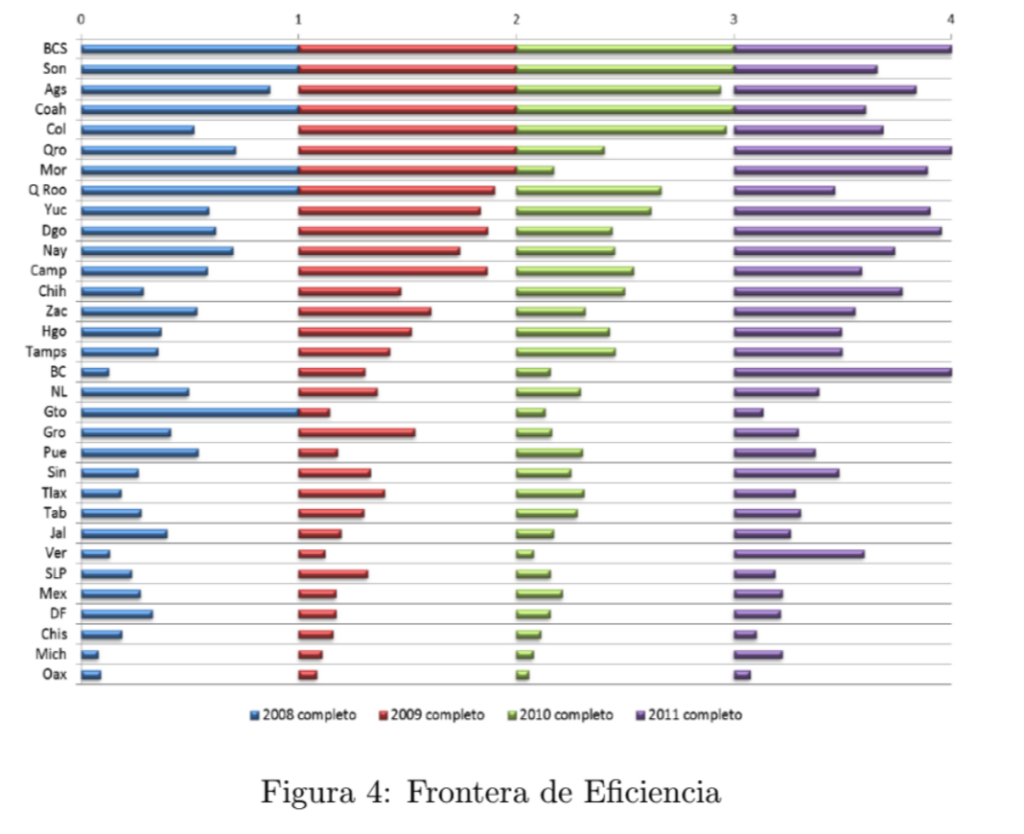
Todos los alumnos de la carrera de matemáticas aplicadas del ITAM asisten a un curso de programación lineal. Aprovechando esto, como el análisis envolvente de datos $(AED)$ se nutre de esa teoría, he tenido el gusto de poder dirigir algunos trabajos de titulación donde se han aplicado las técnicas del $AED$ en diferentes contextos. Estos se encuentran disponibles para consultar en la biblioteca Raúl Baillères Jr., [7]. Uno de los primeros proyectos utiliza el análisis envolvente de datos junto con el coeficiente de Sharp para la selección de acciones para la conformación de carteras de inversiones con buenos resultados. En la tesis [9] se analizó el desempeño de los diferentes estados de la república en el uso de los recursos del Seguro Popular para satisfacer a sus afiliados. De interés es la evaluación de la eficiencia como herramienta para la gestión en el tiempo, como ejemplo, en la Figura 4, se puede ver la variación del desempeño año con año en el periodo analizado $($de 4 años$)$, aunque sí hay una unidad de decisión, Baja California Sur $(BCS)$, que se mantiene eficiente durante todo el periodo. Esta evaluación puede servir para dirigir los esfuerzos de las diferentes entidades y poder observar el tipo de trabajo que se hacen en otros lugares para mejorar el desempeño propio.

La técnica también se puede emplear para ver si los precios de renta y venta de inmuebles son los justos, en [10] se analiza el caso particular de la Colonia Polanco en la Ciudad de México, donde se observó que aquellas propiedades cuya valuación era más eficiente salían más rápido del mercado. En [11] se analizó el desempeño de los 50 diferentes aeropuertos en la república, considerando sus dimensiones capacidades y los servicios de carga y transporte de pasajeros, analizando también las diferencias entre los distintos grupos aeroportuarios del país. En las últimas dos décadas ha habido un crecimiento casi exponencial del número de estudios e investigaciones que emplean esta técnica. Un reto para el lector es encontrar algún estudio que aplique el análisis envolvente de datos a su tema favorito, creo que hay una alta probabilidad de que exista. ¿Al fútbol? existen más de una decena. Para concluir, y recordando el título de este trabajo “¿quién lo hizo mejor?” espero haberles convencido que para contestar esa pregunta de seguro el análisis envolvente de datos puede ayudar.

1. El artículo está considerado como el número 1 entre los 30 artículos más influyentes de los últimos 30 años de la investigación de operaciones en la revista European Journal of Operational Research. ↩︎
2. El nombre de análisis envolvente de datos se debe a que es una técnica que analiza la envolvente de los datos disponibles para evaluar la eficiencia. ↩︎

Referencias

1. W. W. Cooper, L. Seiford , & K. Tone. Data Envelopment Analysis: A Compre- hensive Text with Models, Applications, References and DEA-Solver Software, 2a Edición, Ed. Springer, 2017. ISBN: 978-1489978790 $($492 pp$)$.
2. A. Charnes, W. W. Cooper, E. Rhodes $($1978$)$ “Measuring the Efficiency of Decision Making Units.European Journal of Operational Research”, Vol. 2, pp. 429-444.
3. M.S. Bazaraa, J.J. Jarvis, & H.D. Linear Programming and Network Flows, 4a Edición, Ed. Wiley & Sons, 2019. ISBN: 97804704627720 $($748 pp$)$.
4. AMPL algebraic modeling system. último acceso 31 Enero 2022 https://ampl.com/products/ampl/amplfor-students/
5. A. Charnes & W. W. Cooper $($1962$)$ “Programming with linear fractional functionals«,Naval Research Logistics Quarterly, Vol. 9, No. 3-4, pp. 181-186.
6. Benchmarking package, R project, último acceso 31 Enero 2022 https://www.r-project.org/
7. Biblioteca Raúl Baillères Jr. último acceso 31 Enero 2022 https://biblioteca.itam.mx/new/index.php
8. A. Robles Hüe Una aplicación del análisis envolvente de datos para la selección de acciones para la conformación de carteras de inversión, $($2012$)$ Tesis de la Licenciatura en Matemáticas Aplicadas.
9. M. M. Ramirez Bernal Cálculo de la eficiencia de los recursos del Seguro Popular: una aplicación del análisis envolvente de datos, $($2013$)$ Tesis de la Licenciatura en Matemáticas Aplicadas.
10. E. Gutiérrez Santamaría La eficiencia en el mercado de rentas, una aplicación del análsis envolvente de datos, $($2013$)$ Tesis de la Licenciatura en Matemáticas Aplicadas.
11. J.P. Ortiz Rodríguez Una aplicación del análisis envolvente de datos para el estudio de la eficiencia en los aeropuertos de México, $($2018$)$ Tesis de la Licenciatura en Matemáticas Aplicadas.