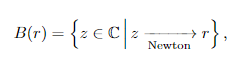La belleza del método de Newton para obtener fractales
Una breve introducción a los fractales
Todos hemos visto un copo de nieve o un helecho y nos hemos fascinado por la forma que siguen estas figuras que nos ofrece la naturaleza. ¿Cómo es posible que el copo de nieve tiene una figura que asemeja a cada parte de sus extremidades $($si es que podemos llamarles así$)$? ¿Cómo es posible que en la hoja de un helecho encontramos la misma figura que tiene la misma hoja? ¿Las hojas de los helechos tienen a su vez hojas de helechos que a su vez tienen hojas de helechos?
Vaya curiosidades tan bellas que nos ofrece la naturaleza. Y es aún más bello poder interpretar esos misterios con matemáticas. Las formas que siguen los objetos que hemos mencionado anteriormente llevan el nombre de fractales. Así, un fractal es una imagen que muestra procesos iterativos que se repiten al infinito. Esto es, un fractal es una figura autosemejante, es decir, es una figura que se parece a cada parte que la compone a diferentes escalas. Por eso nos preguntábamos entonces que, si las hojas de los helechos tienen a su vez hojas de helechos, pues, en efecto, dado que un helecho es un fractal, cada parte de sí asemeja a su vez a un helecho. Lo mismo sucede con un copo de nieve. Parece magia, en efecto, lo que nos ofrece la naturaleza. Y es aún más mágico cuando vemos la gráfica de un fractal.
Pero ¿cómo podemos modelar fractales? ¿cómo puede uno interpretar y crear una gráfica de un fractal? Afirmamos ahora que hay una forma de crear fractales mediante el método de Newton que aproxima las raíces de una función. Y para ello, introduzcamos la motivación de esta afirmación: el problema de Cayley.
Mas antes de enunciar tal problema, recordemos brevemente cómo funciona el método de Newton. Para empezar, el método de Newton es un método numérico que se utiliza para encontrar raíces de una función. Prácticamente, lo que hace este método es, dada una aproximación de la raíz de la función que queremos evaluar con el método, obtener una siguiente aproximación que nace al conseguir la recta tangente a la evaluación de la primera aproximación e intersectando esta recta con el eje $x$.
Dicho método está dado por la sucesión recursiva siguiente. Sea $f(x)$ la función de la cual queremos aproximar las raíces por medio del método de Newton. Luego, dada una aproximación inicial $x_0$ de la raíz, las siguientes aproximaciones más cercanas a la raíz se dan por la fórmula:
$$ x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}$$
El problema de Cayley
El matemático inglés Arthur Cayley propuso, en el siglo XIX, utilizar el método de Newton para encontrar raíces de una función definida en el plano complejo. Esto es, se propuso resolver, con el método de Newton, la ecuación siguiente:
$$
f(z) = 0, \textrm{ donde } f: \mathbb{C} \rightarrow \mathbb{C}
$$
Pero, ¿cómo utilizamos el método de Newton para encontrar raíces de una función compleja? Fácil, el método de Newton se generaliza de forma directa al campo complejo. Esto es, dada una aproximación inicial $z_0$ de la raíz compleja $z$, las siguientes aproximaciones más cercanas de la raíz se dan por la fórmula:
$$z_{n+1} = z_n – \frac{f(z_n)}{f'(z_n)}$$
Pero Cayley no quería solo encontrar las raíces de funciones o polinomios definidos en el campo complejo mediante el método de Newton. Eso, hasta cierto punto, es algo trivial. Cayley quiso analizar el comportamiento de algo que será la base de este pequeño trabajo: las cuencas de atracción.
Espera, ¿qué? ¿Una cuenca de atracción? Definamos entonces lo que es una cuenca de atracción. Sea $r$ una raíz de la función de nuestro interés, llamémosle a esta $f(z)$. Se define la cuenca de atracción de $r$ como el conjunto de todos los números $z$ tales que, si empezamos el método de Newton en esa $z$, el método converge a la raíz $r$ de nuestro interés. Se denota como $B(r)$ a la cuenca de atracción de la raíz $r$. Esto es, en términos matemáticos, tenemos que la cuenca de atracción de la raíz $r$ es el conjunto siguiente:
donde la flecha representa la convergencia del método de Newton al aplicarlo sobre el valor inicial $z$.
Esta definición nace de la siguiente observación. Si una función tiene varias raíces $($tanto en los reales como en los complejos$)$, no todas las aproximaciones iniciales que tomemos nos llevarán a las mismas raíces al usar el método de Newton. Esto es, puede existir una $x$ que nos mande a la primera raíz, y otra $x$ en el espacio en que estamos trabajando que nos mande a la segunda raíz. Por ello necesitamos la definición de cuenca de atracción, para poder identificar este fenómeno.
Dada esta definición, estamos listos para enunciar el problema de Cayley. Cayley, en 1879, publicó en la revista American Journal of Mathematics lo que él llamó como el problema imaginario de Newton-Fourier. Dicho problema consiste en analizar las cuencas de atracción cuando el método de Newton es usado para encontrar o aproximar las raíces del polinomio complejo que denotaremos por $p(z)$. Esto es, parafraseando a Cayley, dado un polinomio $p(z)$ con raíces $A_1,A_2,A_3,\ldots$, y los valores iniciales de aproximación $P_0,P_1,P_2,\ldots$ seleccionados al gusto, el problema es determinar las regiones del plano complejo tales que $P_i$ nos lleva a la raíz $A_j$.
Cayley, en el mismo artículo, menciona que la solución es “fácil y elegante” para el caso del polinomio cuadrático $p(z)=z^2-1$. Incluso probó que las dos cuencas de atracción subdividen al plano complejo en dos regiones iguales, donde cada región corresponde a cada cuenca de atracción. Pero que, en el caso del polinomio cúbico, $p(z)=z^3-1$, el problema parece sumamente complicado. Intentó resolver el problema por varios años, pero, sin lograr resolverlo, concluyó que eran demasiadas operaciones y cálculos; lo dejó planteado como problema.
Pobre e inocente Cayley. No sabía que tenía enfrente de sí un fractal. Por supuesto que el problema para el polinomio cúbico es sumamente complicado, pues al analizar las cuencas de atracción de dicho polinomio a sus respectivas raíces, obtenemos nada más y nada menos que un fractal. ¿Cómo sabemos ahora esto? Hoy, podemos resolver el problema que Cayley tenía: demasiadas operaciones. Hoy tenemos programas y computadoras que nos permiten realizar una cantidad impresionante de operaciones en cuestión de segundos. Y no sólo eso, también tenemos graficadoras sumamente precisas que nos permiten observar el comportamiento de las cuencas de atracción del polinomio mencionado. Así que resolvamos el problema de Cayley.
Un acercamiento del comportamiento fractal
Antes de resolver el problema de Cayley, veamos una intuición en los reales, sin considerar al plano complejo, que nos ayude a entender cómo se está dando el comportamiento fractal, y que nos dé además el algoritmo para resolver el problema de Cayley.
Consideremos entonces la función $f(x)=x^3-x$. Dicha función tiene tres raíces bastante sencillas: $-1$, 0, 1. Denotemos a dichas raíces como $r_1, r_2$ y $r_3$,respectivamente. Analicemos ahora qué pasa con las cuencas de atracción. ¿Por qué todo esto? ¿A dónde nos va a llevar el análisis de las cuencas de atracción? Abusaremos de que el método de Newton, como todo método numérico, no siempre convergerá de forma cuadrática, o no siempre se comportará como nosotros queremos dada una función que elijamos. Elegimos una función que precisamente hará llorar al método de Newton. $($¿Puede llorar?$)$
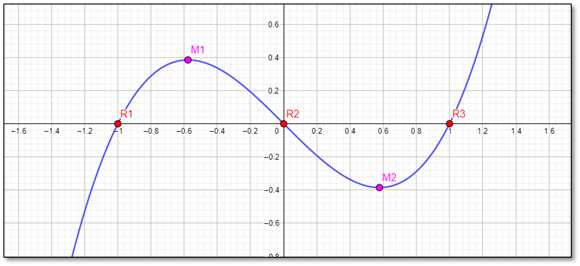
En primer lugar, veamos cómo se ve la gráfica de dicha función.
En la gráfica superior, observamos el comportamiento de la función que estamos analizando. Los puntos en rojo corresponden a las tres raíces del polinomio, y los puntos en rosa representan los extremos locales con los que estaremos trabajando. Empecemos entonces a analizar las cuencas de atracción. En primer lugar, observamos que cualquier punto antes del extremo $M_1$ convergerá $r_1$ $($la raíz $-1$ $)$ al aplicarle el método de Newton. Esto es directo de observar cómo funciona dicho método para los puntos antes del extremo de manera geométrica, pues las rectas tangentes de estos puntos nos acercarán más a la raíz. Podemos ver esto con un ejemplo.
Supongamos que tomamos $x_0=-2$. Tras iterar una vez el método de Newton, obtendremos que la primera aproximación es $x_1=-1.4545$. Iterando de nueva cuenta el método, obtendremos que la siguiente aproximación es $x_2=-1.1510$. Vemos así que nos estamos acercando a la primera raíz del polinomio que estamos trabajando. Así, podemos entonces decir que los puntos antes del extremo $M_1$ pertenecen a la cuenca de atracción de la primera raíz, $-1$. Esto es, para toda $x < M_1$, se cumple que $x \in B(r_1)$. De manera análoga podemos concluir que para toda $x > M_2$, se cumple que $x \in B(r_3)$, pues la función que tenemos entre nosotros es simétrica. En los extremos, dado que la derivada en esos puntos es cero, el método de Newton no converge a ningún lugar, entonces no podemos incluir a los extremos en ninguna cuenca de atracción.
Ahora, ¿qué pasara con los puntos después de $M_1$ y antes de $M_2$? Aquí es donde empezaremos a analizar cosas curiosas. Tomemos, por ejemplo, el punto $y_0=-0.5$ como aproximación inicial e iteremos el método de Newton para ver qué sucede. Tras realizar una sola iteración del método de Newton, obtenemos que la siguiente aproximación es $y_1=1$. Llegamos a la raíz, pero, lo más interesante de esto es que nos pasamos del otro lado del eje ordenado y llegamos a $r_3$. Así, podemos decir entonces que $y_0 \in B(r_3)$. Sorprendente, pues dicho punto era negativo. De nuevo, de manera análoga, podemos observar que el punto 0.5 converge a $-1$ y, por tanto, dicho punto pertenece a la cuenca de atracción $B(r_1)$.
Entonces, si seguimos disminuyendo el valor de los puntos, ¿podemos esperar un comportamiento similar? Primero que nada, ya vimos que antes de $M_1$, los puntos convergen a $-1$. Tomamos un punto después de $M_1$, $-0.5$, y vimos que convergió a 1. ¿Podemos esperar que, si tomamos un punto más cercano a cero, supongamos $a_0=-0.46$, seguirá convergiendo a la raíz 1? Veamos entonces, para dejar de especular. Apliquemos el método de Newton al punto dicho. Tras varias iteraciones, llegaremos a que dicho punto converge a $-1$. ¡Vaya comportamiento! Hemos observado entonces que regresamos a la cuenca de atracción $B(r_1)$. Este comportamiento seguirá así. Si tomamos ahora $b_0=-0.4485$, dicho punto convergerá ahora a 1; entonces $b_0\in B(r_3)$.
¿Qué estamos observando entonces? ¿Qué nos está indicando este
comportamiento? Cambiar un poquito nuestra elección de puntos provocará que el
método de Newton converja a una raíz completamente distinta. Pequeños cambios en
la aproximación inicial del método resultarán en un cambio de cuenca de atracción
drástico.
Ahora, ¿cuál es la magia de todo esto? ¿Por qué estamos aventando números, convergencias y cuencas al azar? ¿De qué nos sirve analizar este comportamiento sensible de la función considerada? Aguánteme un segundo, y veamos entonces qué está pasando con las cuencas de atracción.
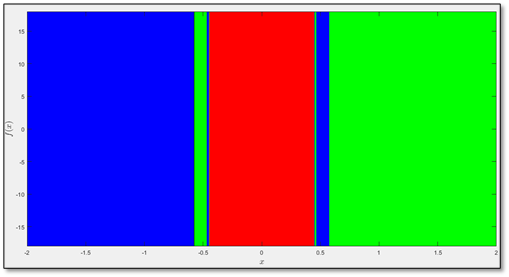
Lo que haremos ahora es colorear todos los puntos de $B(r_1)$ de azul, todos los puntos de $B(r_2)$ de color rojo y todos los puntos de $B(r_3)$ de color verde. ¿Y qué obtendremos? Obtendremos nada más y nada menos que lo que estábamos buscando: un fractal. Este fractal, dado que lo que estamos coloreando son puntos en $\mathbb{R}$, sería en realidad una gráfica de una dimensión, lo cual no nos permitiría ver propiamente el comportamiento fractal. Por ello, graficamos el fractal en dos dimensiones, aunque propiamente el fractal solo aparece en la recta. Veamos entonces cómo se ve este fractal tan mencionado.
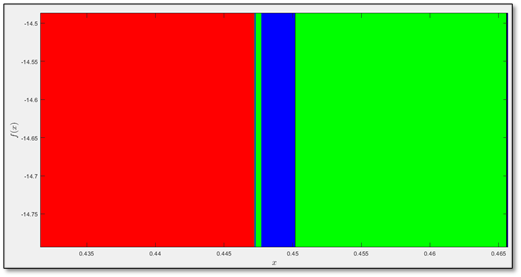
Observamos que la parte central corresponde a la cuenca de atracción $B(r_2)$, esto es, son los puntos que convergen con el método de Newton al cero. Los grandes cúmulos de azul y verde corresponde a las cuencas de atracción $B(r_1)$ y $B(r_3)$, respectivamente. Estas últimas dos cuencas corresponden al primer análisis que hicimos: son los puntos antes del extremo $M_1$ y después del extremo $M_2$, respectivamente. Estas tres zonas podemos decir que no son de nuestro interés, pues solo son una plasta de color. Lo que nos interesa a nosotros es la franja que aparece alrededor del valor 0.5 y $-0.5$. Ahí es donde se está presentando el comportamiento fractal que tanto hemos mencionado. Ahí es donde vimos que, con pequeños cambios en nuestra aproximación inicial, el método de Newton convergió a diferentes raíces. Hagamos un acercamiento a esa zona para observar el comportamiento fractal.
El acercamiento mostrado arriba se parece tremendamente a la imagen completa. ¿Hicimos en realidad un acercamiento? ¿Cómo sabe usted, lector, que simplemente no cambiamos las etiquetas de los ejes de la gráfica original y pusimos esa edición aquí? Bromas aparte, el acercamiento de arriba precisamente nos muestra lo que queríamos: el comportamiento fractal. Nos hemos acercado en la imagen y hemos llegado a la misma imagen, pero en una escala menor. Si nos seguimos acercando a la imagen, encontraremos de nuevo la misma imagen. Hemos encontrado así una figura autosemejante. Hemos encontrado así un fractal. Pero, un momento, ¿cómo estuvo eso de colorear las cuencas de atracción? ¿cómo colorea uno un conjunto? Expliquemos entonces el algoritmo de cómo colorear las cuencas de atracción. Esto nos servirá más adelante para resolver el problema de Cayley.
El algoritmo para colorear las cuencas es bastante sencillo. Se basa en la pregunta que podemos llamar ya fundamental: si agarro un punto del espacio, dada una función, ¿a qué raíz de la función convergerá este punto si le aplicamos el método de Newton? Supongamos que tenemos $f(x)$ nuestra función de interés con raíces $r_1,r_2,r_3,\dots,r_n$.Tomemos $x_0$ como nuestra aproximación inicial, y supongamos que mediante el método de Newton converge a un valor $\tilde{x}$. Sea $\varepsilon > 0$ la tolerancia que vamos a tener entre nuestra aproximación y la raíz real $($el error que toleramos$)$. Nos preguntamos ahora, ¿es la distancia entre $\tilde{x}$ y $r_1$ menor a la tolerancia dada? Esto es, en términos matemáticos, ¿$|\tilde{x} – r_1| < \varepsilon$? Si sí, entonces nuestro punto inicial $x_0$ converge a $r_1$, esto es, $x_0 \in B(r_1)$.
Entonces, lo que hacemos es colorear a este punto de un color que represente a todos los puntos que convergen a la primera raíz, digamos que es el azul. Pero, ahora, si la distancia entre $\tilde{x}$ y $r_1$ no fue menor a nuestra tolerancia dada, entonces repetimos el proceso con la siguiente raíz. De nuevo, si sí converge a $r_2$, entonces coloreamos al punto ahora de otro color que represente a todos los puntos que convergen a la segunda raíz, digamos que es rojo. Repetimos este proceso hasta encontrar a qué raíz converge nuestra primera aproximación. Si, en el peor de los casos, nuestra primera aproximación hace llorar al método de Newton y no converge a ninguna raíz, entonces pintamos a nuestro punto de otro color especial que nos ayude a diferenciar si un punto no converge a ninguna raíz. Así, al final de este proceso, que parece cansado, tendremos coloreada a nuestra aproximación inicial, esto es, tendremos ubicada a nuestra aproximación inicial en su respectiva cuenca de atracción.
Repetimos este proceso con diferentes aproximaciones iniciales y, así, obtenemos las cuencas de atracción coloreadas que nos permitirán observar gráficamente el comportamiento de las cuencas de atracción. El modo en que implementamos este algoritmo se vislumbra en los códigos adjuntos. Con este algoritmo, vimos que la función $f(x)=x^3-x$ generó un fractal al colorear las cuencas de atracción. Pero, como mencionamos previamente, la imagen de este fractal es una imagen de “una dimensión”, pues el fractal solo se da con puntos que tienen una coordenada: los puntos reales. Entonces puede que no generemos imágenes tan bonitas si trabajamos con puntos reales. ¿Por qué no mejor trabajar con puntos complejos? ¿Cómo? ¿Puntos complejos? Si trabajamos con puntos complejos, tendremos que nuestros puntos de las cuencas de atracción serán números complejos, que se pueden representar en el plano complejo, un plano que podemos visualizar como una gráfica de dos dimensiones. Entonces podremos visualizar un fractal en dos dimensiones. ¡Vaya imágenes tan magníficas ya visualizamos en nuestras mentes! Además, si trabajamos con puntos complejos, de paso resolveremos el problema de Cayley.
¿Era problema el de Cayley?
Dado que ya conocemos el algoritmo de cómo colorear cuencas de atracción, si trabajamos con puntos complejos, podemos entonces encontrar las cuencas de atracción del problema de Cayley. Podemos ahora encontrar las cuencas de atracción de $p(z)=z^3-1$. Y no solo de este polinomio, también de muchos otros polinomios complejos que sigan una estructura similar. ¿Por qué Cayley no pudo entonces encontrar las cuencas de atracción? Parece un procedimiento sencillo, sí; lo es, para un matemático promedio del siglo XXI que cuenta con paquetes masivos de programación que permiten realizar tantas operaciones y crear imágenes precisas de lo que está pasando: el comportamiento fractal. Pero Cayley no contaba con todos estos recursos para dibujar fractales. Es más, en ese entonces, la teoría de los fractales $($y, es más, la teoría de sistemas dinámicos$)$ apenas agarraba forma. Entonces ¿era problema el de Cayley? ¿Se le puede acusar de no haber resuelto el problema cuando no tenía las armas para trabajar con fractales?
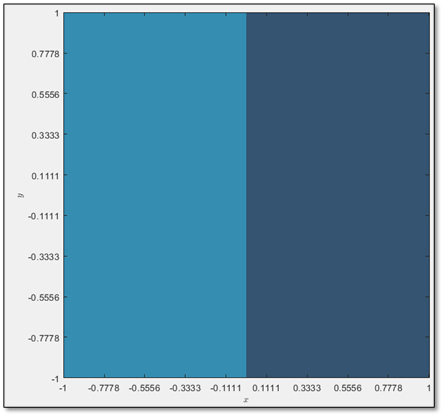
Antes de contestar dicho problema, y dibujar las cuencas de atracción para el polinomio mencionado, reiteremos lo que Cayley ya había demostrado. El matemático mencionaba que encontrar las cuencas de atracción para el polinomio $p(z)=z^2-1$ es “fácil y elegante”. Veamos entonces por qué decía esto el abogado. Dicho polinomio tiene solo dos raíces: 1 y $-1$.
Antes de interpretar el resultado de la gráfica, es importante recordar que un número complejo se escribe de la forma $z=a+bi$, donde $i$ es la unidad imaginaria $(\sqrt{-1})$ y $a,b\in \mathbb{R}$. A $a$ se le conoce como la parte real del número complejo y a $b$ se le conoce como la parte imaginaria del mismo. Para graficar el número complejo $z$, se grafica el par ordenado $(a,b)$ en lo que se conoce como el plano complejo. Esto es, la gráfica es prácticamente análoga al plano $\mathbb{R}^2$, solo que, en el caso del plano complejo, el eje vertical corresponde a la parte imaginaria del punto y el eje horizontal corresponde a la parte real del punto. Así, lo que estamos observando en la gráfica de arriba es el plano complejo, que contiene puntos del campo complejo representados con sus dos componentes, el componente real y el componente imaginario. Esa ventaja, que los números imaginarios se puedan representar en una gráfica de dos dimensiones, es la que se está abusando aquí.
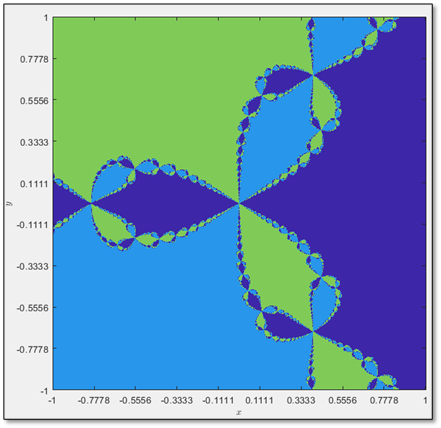
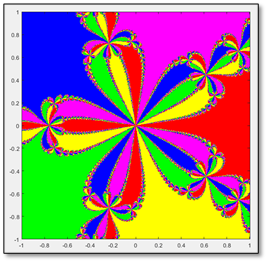
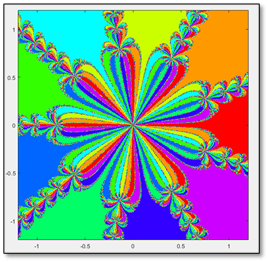
Observamos que las cuencas de atracción de $p(z)=z^2-1$ dividen al plano complejo en exactamente dos mitades. Es justo lo que Cayley había concluido hace unos ayeres. Observamos también que es una gráfica bastante aburrida. No presenta ningún comportamiento que llame nuestra atención ni mucho menos. Es por ello por lo que Cayley pudo concluir lo que concluyó, pues no hay ningún comportamiento extraño en ese caso. Ahora sí, después de tanta palabra, resolvamos el problema de Cayley. Dibujemos, con todo lo que ya sabemos, las cuencas de atracción del polinomio $p(z)=z^3-1$. Esperamos tres regiones con colores distintos, pues dicho polinomio, al ser de grado 3, tiene tres raíces $($ya sea reales o complejas$)$.
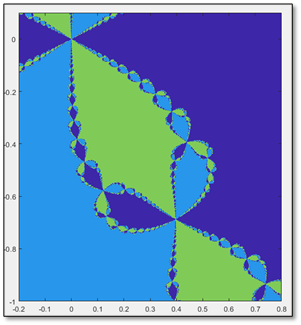
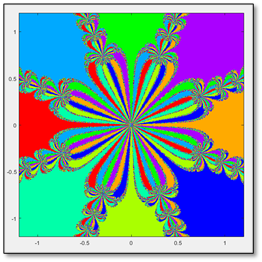
¡Sorpresa! ¿Qué estamos observando ahora? Observamos ahora un comportamiento sumamente diferente al comportamiento observado en el polinomio de caso cuadrático. Vislumbramos ahora el comportamiento fractal. Al fin, llegamos al final del edificio que hemos estado construyendo. Descubrimos ahora por qué Cayley pasó años sin resolver el problema: semejante comportamiento no es intuitivo de descubrir sin el uso de métodos numéricos y procesadores de datos. Notamos que es una figura autosemejante. ¡Es un fractal! Cada uno de los pequeños blobs, vuelve a aparecer en sí mismo $($véase la figura 6$)$. Y en sí mismo. Y en sí mismo. Vaya belleza de la naturaleza, sin duda alguna. Es así como hemos resuelto el problema de Cayley. Hemos logrado colorear las cuencas de atracción del polinomio $p(z)=z^3-1$ y hemos descubierto el comportamiento fractal que se escondía tras ellas, que tantas pesadillas dio a Cayley.
¿Eres matemático y siempre supiste que tu pasión era el diseño gráfico?
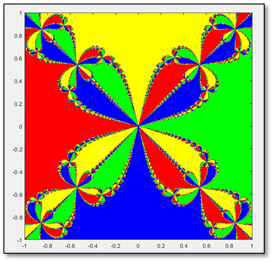
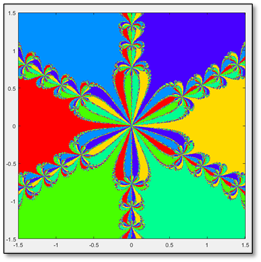
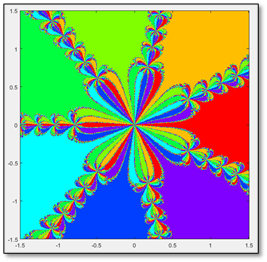
No nos quedemos en solo analizar las cuencas de atracción del polinomio dicho. Ya tenemos toda un arma para analizar cuencas de atracción de muchos más polinomios. Veamos entonces qué sucede al aplicar todo lo que sabemos a otros polinomios. ¡Juguemos con los fractales!
Conclusiones, comentarios y advertencias
¡Vaya forma tan preciosa de generar imágenes de la naturaleza! ¡Vaya curiosidades tan bellas que nos ofrece la naturaleza! No solo hemos resuelto el problema de Cayley de una manera bastante sencilla, sino que también creamos un algoritmo que genera imágenes bastante divinas. El problema de Cayley era un problema de tiempo. Seguramente dicho maestro matemático hubiera logrado resolver su propio problema si contara con métodos numéricos y máquinas que le permitieran entender el comportamiento fractal que estaba intentado descifrar con un lápiz.
¡Vaya, además, aplicaciones de un método que parecía solo funcionar para aproximar raíces! Quién diría que el método de Newton podría generar fractales tan preciosos y bonitos. Así que, si eres matemático, pero siempre supiste que lo tuyo era el diseño gráfico, ¡ya sabes qué hacer! ¡Junta las dos materias!
Como advertencia al lector: asegúrese de que su computadora tiene suficiente capacidad para correr los fractales, si es que usted desea adaptar el algoritmo. La cantidad de datos que se procesan puede destruir su computadora. Tenga usted cuidado.
Bibliografía
- Burton, Aaron (2009).“Newton’s Method and Fractals”
http://www.whitman.edu/documents/Academic/Mathematics/burton. - Castañeda, Pablo. Matemática Computacional 14390-001, Capítulo 3 Localización de
raíces y extremos locales. ITAM, 2021. - Cayley, Professor. Desiderata and suggestions: no. 3. The Newton-Fourier imaginary pro-
blem. American Journal of Mathematics 2.1, 1879: 97. - Mónica Oviero, Ana María Kanashiro y Mauro Colombini. Fractales. Un universo poco
frecuentado. Univerdidad Nacional del Litoral, 2005. - Plazas Salinas y Gutiérrez Jiménez. Dinámica del Método de Newton. Universidad de las
Riojas, 2013. - Rubiano, Gustavo ”Método de Newton, Mathematica y Fractales: Historia de una pági-
na” Boletín de matemáticas 12, no. 14.1 (2007): 44-63. - Talanquera, Vicente Fractus, fracta, fractal: fractales, de laberintos y espejos. Fondo de
cultura económica, 2011.