Rescatando lo más importante

El valor absolutivalizado se quiere desabsolutivalizar y el que bien lo desabsolutivalice un buen desabsolutivalizador será

César Luis García García

…y eso que apenas son las 9:00

Sobre la SVD

La descomposición en valores singulares $($SVD, por sus siglas en inglés$)$ es una factorización que se le puede hacer a cualquier matriz $A\in M_{m\times n}(\mathbb{R})$. Dicha descomposición está dada de la siguiente manera:
\[
A = U\Sigma V^T\:,
\]
en donde $U\in M_{m\times m}(\mathbb{R})$, $V\in M_{n\times n}(\mathbb{R})$ y $\Sigma \in M_{m\times n}(\mathbb{R})$. La matriz $\Sigma$ tiene la siguiente forma:
\[
\Sigma = \begin{pmatrix}
C & \overline{0}\\
\overline{0} & \overline{0}
\end{pmatrix} ;
\]
y la matriz $C$ es una matriz diagonal con entradas $\{\sigma_1,\sigma_2,\cdots,\sigma_k\}$. Aquí, $k=rank(A)$. Estos valores $\sigma_i$ se llaman valores singulares de $A$.

En pocas palabras, el presente texto no pretende enseñar cómo se llega a dicha descomposición.  Más bien nos interesa revisar algunas de sus aplicaciones.

Sean $u_1$, $u_2$, …, $u_m$ las columnas de la matriz $U$ $($a veces llamados vectores singulares izquierdos$)$ y sean $v_1$, $v_2$, …, $v_n$ las columnas de $V$ $($a veces llamados vectores singulares derechos$)$. Nótese que podemos hacer la siguiente reducción:
\begin{equation}
\begin{aligned}
U\Sigma V^T
& =
\begin{pmatrix}
\sigma_1 u_1 \mid \sigma_2 u_2 \mid \cdots \mid \sigma_k u_k
\end{pmatrix}
\begin{pmatrix}
v_1^T\\
v_2^T\\
\vdots\\
v_n^T\\
\end{pmatrix}\\
& = \sum_{i=1}^k \sigma_i u_iv_i^T
\end{aligned}\:.
\label{eq}
\end{equation}
En otras palabras, la SVD nos permite escribir cualquier matriz como suma de matrices de rango 1 $($recordemos que el producto exterior $ab^T$ de dos vectores $a$ y $b$ conforma una matriz de rango $1$$)$. La idea detrás de muchas aplicaciones de la SVD proviene de esta suma. Hay dos razones.

Primero, reducimos la dimensión. Esta aplicación es muy común en estadística bajo el nombre de componentes principales.
¿Cómo visualizamos un objeto de dimensión alta en $\mathbb{R}^2$? Muchas veces, esta visualización gráfica permite tomar decisiones. Un ejemplo se proveé en la sección Descifrando un Texto

Segundo, como ya se mencionó, las matrices de rango 1 requieren dos vectores $($$u_i, v_i$$)$ y un escalar $($$\sigma_i$$)$. Además, en la práctica, los primeros valores singulares tienden a ser mucho mayores que los demás.
En consecuencia, podemos quedarnos con solo los primeros $r$ términos en la suma anterior y tendremos una matriz parecida a $A$. Pues, es posible almacenar mucha información $($si $A$ es una matriz de dimensiones grandes$)$ en unos pocos vectores.
En la sección Aproximando una Imagen damos un ejemplo de esto. Pero antes…

Aproximando a $A$

Definición
Sea $A$ una matriz de $m\times n$ entradas.
Luego, la aproximación a $A$ de rango $r$ por valores singulares es
\[
A_r = \sum_{i=1}^r \sigma_i u_i v_i
\]

Descifrando un Texto

Figura 1: Graficamos $u_2$ contra $v_2$ para el texto encriptado

¿No detestas cada vez que estás leyendo un libro y, en el momento más tenso del clímax, te percatas de que hay una página encriptada? ¡No desesperes más! Los valores singulares pueden ayudarte a desencriptar ese texto. Es muy sencillo. Construimos una matriz $M$ en la que $(M)_{i,j}$ es la frecuencia con la que la $i-$ésima letra precedió a la $j-$ésima letra en el texto. En la palabra constatar, por ejemplo, $(M)_{21,1}=2$ ya que la a $($letra 1$)$ sigue a la t $($letra 21$)$ dos veces exactamente. Pues, construimos nuestra matriz $M$ ignorando espacios, puntuaciones y acentos. También suponemos que el texto es cíclico, de manera que la última letra precede a la primera.

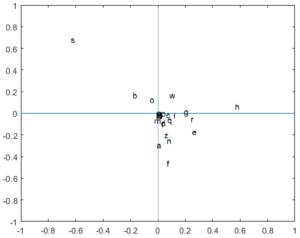
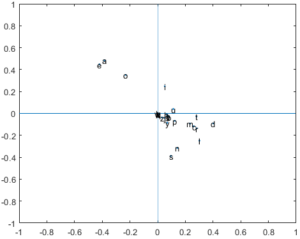
Aplicando una descomposición en valores singulares a $M$, graficamos $u_2$ contra $v_2$ y obtenemos la Figura 1. Aplicamos ahora el mismo procedimiento a un pasaje que esté redactado en español ordinario.
Obtenemos la Figura 2. No es azar que las vocales a, e, o estén todas en el segundo cuadrante. Según Moler $($1983$)$, esto es lo que pasa para los idiomas que siguen la regla vfc $($vowel follows consonant$)$.

Figura 2: Graficamos $u_2$ contra $v_2$ para un texto en español

Definición
La regla vfc se cumple en un texto cuando
\[
\frac{\textit{Número pares vocal-vocal}}{\textit{Número de vocales}}<\frac{\textit{Número de pares consonante-vocal}}{\textit{Número de consonantes}}
\]

Cuando un texto o un idioma sigue la regla vfc, las vocales están en el cuadrante dos y las consonantes en el cuadrante cuatro.
Para una demostración de esto, consultar Moler. Pues, podemos estar muy seguros de que en el mensaje encriptado, las letras s, o, y b representan a la a, e, y o, en algún orden. ¿Por qué la u y la i no siguen esta regla de clasificación? El español no es, en general, un idioma vfc. Hay muchos pares de vocal vocal que empiezan con la letra u $($quien, cuando, que, huevos, tuerto$)$ o con la letra i $($siento, bien, miel, quien, cien$)$. Todas estas palabras en el español impiden que se cumpla la regla vfc. Sin embargo, al no haber tantos casos de diptongos que comiencen con la a, la e o con la o, estas tres vocales sí siguen la regla vfc.

Aproximando una imagen

En esta sección utilizamos una imagen de Sofía Kovalévskaya, matemática rusa. Esta imagen, en blanco y negro, puede ser vista como una matriz $A\in M_{326\times 259}(\mathbb{R})$. En cada entrada tiene un entero entre 0 y 255 que determina el tono de gris que ocupa un pixel.

Los valores singulares de $A$ decrecen rápidamente.

Figura 3: Sofía Kovalévskaya en diferentes rangos

En la Figura 3 podemos observar cómo hay un solo valor singular de tamaño mayor a $10^4$, apenas una decena mayor a $10^3$ y el resto son menores a $10^3$. Esto, en otras palabras, quiere decir que la gran mayoría de la información está concentrada en tan solo los primeros valores y vectores singulares. Pues, tomamos $A_r$ para distintas $r$ y vemos qué tanto se ven como $A$. En la figura anterior  observamos cómo se comparan $A$, $A_1$, $A_{20}$
y $A_{50}$. Nótese cómo una aproximación de dimensión 50 es bastante cercana a la original. En términos reales, acabamos de reducir drásticamente la información necesitada para guardar la imagen sin perder mucha infromación. Mientras que la imagen original ocupa $326\times 259 = 84,434$ entradas, una imagen de rango $r$ necesita almacenar unicamente las entradas de los $r$ primeros vectores singulares $($izquierdo y derecho$)$, además de los $r$ valores singulares. Es decir, necesitamos $r(259+326+1)$ entradas. Para $r=50$, estas son $29,300$ entradas. Guardamos menos de la mitad de la información y el resultado es casi idéntico.

¹Calderón de la Barca, Pedro$($1635): La vida es sueño, Clásicos² Moler, Cleve $($2004): Numerical Computing with MATLAB Society for Industrial and Applied Mathematics³ Moler, Cleve y Morrison, Donald $($1983): Singular Value Analysis of Cryptograms, The American Mathematical Monthly Vol. 90, número 2, pp. 78-87. ⁴ Sofia Vasilyevna Kovalevskaya, Consultado el 4 de mayo del 2020. http://mathshistory.st-andrews.ac.uk/Biographies/Kovalevskaya.html