En la actualidad, el transporte público en la Ciudad de de México no tiene la capacidad para transportar a todas las personas que desean hacerlo por este medio, lo que ocasiona diferentes problemas en la capital; tales como congestión vehicular, contaminación por uso de vehículos particulares o taxis, inseguridad en las estaciones de transporte público, y períodos largos de viaje para los ciudadanos que utilizan transporte público o privado. Un estudio de Moovit Insights muestra que, en promedio, las personas tienen un tiempo de viaje de 88 minutos y el 89% de los usuarios dedican aproximadamente 2 horas para los desplazamientos diarios. En 2016, el director del Sistema de Transporte Colectivo $($STC$)$, Jorge Gaviño, mencionó que el la red del metro tenía capacidad para recibir a 3 millones de usuarios y estaba recibiendo en cambio a 5.5 millones, resultando en un sobrecupo de 2.5 millones de usuarios. Como los recursos son limitados y hay pocas oportunidades para ampliar el sistema en el corto plazo, una manera de mejorarlo es proporcionar una administración adecuada por medio de políticas de viaje.
En lo que sigue se modela la dinámica del tiempo de llegada y el flujo de los pasajeros como variables estocásticas, en particular, como procesos Poisson. Conocer a detalle la dinámica podrá ser de ayuda para implementación de políticas de viaje, políticas públicas y programas de regulación viajera.
Desarrollo del Modelo
En 2005, Germán Riaño propuso un modelo para resolver un problema de Programación Lineal de Optimización para el transporte país. Riaño esperaba minimizar el número de rutas que se utilizan en una red de autobuses como sistema de transporte colectivo basado en la frecuencia de salida de los autobuses para economizar gastos gubernamentales mientras se mantiene cierta calidad de servicio para los pasajeros y se satisface un nivel de demanda. A pesar de que el modelo se basa en autobuses, Riaño especifica que el modelo debería de funcionar para cualquier otro sistema de transporte urbano masivo con paradas fijas, siempre y cuando la frecuencia de operación sea lo suficientemente alta para que los pasajeros no necesiten conocer de antemano los horarios $($en caso de existir$)$ y, por lo tanto, lleguen de manera independiente a la estación o parada.
| Concepto | Dato* |
| Tiempo promedio de viaje | 88 minutos |
| Tiempo promedio de espera en una parada | 11 minutos |
| % de personas que esperan más de 20 minutos en la estación | 14 % |
| Distancia promedio de viaje en transporte público | 9.9 km |
| Promedio de llegada de personas por estación $($en un sentido$)$ | 8.8 miles |
| Lı́neas de metro en la CDMX | 15 lı́neas |
| Estaciones en la lı́nea 7 | 14 estaciones |
| Trenes en la lı́nea 7 | 33 trenes |
| Trenes disponibles $($en una sola dirección$)$ | 12 trenes |
| Capacidad de personas por tren | 1530 personas |
| Tiempo de recorrido entre estación por tren | 3 minutos |
Cuadro 1: Algunos datos de la Red del Sistema de Transporte Colectivo de la CDMX
Definiciones y supuestos
El modelo de Riaño se basa principalmente en el comportamiento intrínseco de dos variables:
- La demanda de los pasajeros mientras estos arriban a la estación.
- El tiempo de viaje o de desplazamiento.
Lo importante de la consideración de estas dos variables radica en lo fluctuante que resultan ser en el tiempo y la variabilidad de estas una vez que se fija un periodo, por lo cual pueden considerarse como procesos estocásticos.
Supondremos que el día está dividio en periodos definidos como intervalos de la misma longitud, de tal modo que nos referimos al intervalo $(t-1,t]$ como el periodo~$t$. Cada estación o parada del metro será referida por $i=0,1,\ldots,N$ donde el recorrido entre dos estaciones consecutivas, $i-1$ e $i$, es el segmento $i$. Denotaremos a $x_{it}$ como la frecuencia con la que salen los trenes de la estación $i$ en el periodo $t$. Entonces, la variable de decisión del modelo es $x_{0t}$ pues la dinámica de las frecuencias $x_{it}$ para $i=1,\ldots,N$ dependerá de la frecuencia de la estación anterior en cada periodo. Además, el número de trenes se mantiene constante $K$ y la oferta mínima aceptable en la estación $i$ durante el periodo $t$ la representamos $\theta_{it}$. De esto último podemos fijar una restricción de servicio:
$$Kx_{it}>\theta_{it}$$
lo cual garantiza que la demanda de transporte se satisfaga.
Se puede demostrar que si $x_{0t}$ se mantiene constante en cada periodo $t$, entonces la frecuencia $x_{it}$ se puede escribir como $$x_{it}=\sum\limits_{s=1}^t w_{s}^{t}(i)x_{0t}, \qquad \forall t, i=0\ldots n$$
donde $w_{s}^{t}(i)$ es la fracción de trenes que salieron de la estación $0$ en el periodo $s$ y pasaron por la estación $i$ en el periodo $t$. En cuanto al comportamiento de los pasajeros, supondremos que la demanda de pasajeros llega a cada estación de acuerdo a procesos de Poisson no homogéneos. Además, el número total de pasajeros que pasan por el segmento $i$ durante el periodo $t$ es una variable Poisson.
El modelo de Riaño supone que los tiempos de desplazamiento entre estaciones tienen una distribución normal. Este supuesto se hace por conveniencia ya que facilita el cálculo. Sin embargo, una distribución normal puede tomar tiempos negativos y cuando esto sucede se programan excepciones para que se tomen tiempos positivos lo cual podría afectar, aunque de manera no tan significativa, los resultados. Para evitar estas excepciones en la programación de la simulación, usaremos una distribución exponencial que tiene una relación con la distribución Poisson.
La demanda se supone que llega de acuerdo a procesos de Poisson independientes no homogéneos. Denotaremos a $\lambda_{ij}(\tau)$ la tasa de arribos a la estación $i$ con rumbo $j$ hasta el instante $\tau$. Para simplificar la situación, supondremos tasas constantes en los períodos, es decir, $$\lambda_{ij}(t)=d_i^j(t),$$
donde $d_i^j(t)$ es la tasa a la cual se origina la demanda en la estación $i$ a la estación~$j$, y la tasa variable de arribos a la estación $i$ viene dada por $$\lambda_i(\tau)=\sum_{j>i}\lambda_{ij}(\tau).$$
Modelado de los tiempos de viaje
\noindent Llamaremos $T_{ik}$ el tiempo que tome el $k$-ésimo tren para ir de $i$ a $i+1$ que se distribuye exponencial con parámetro $\mu$ donde se tiene que $$S_{ik}=\max\left(S_{i-1,k}+T_{ik}, S_{i,k-1} \right)$$
con $S_{ik}$ la hora de salida del $k$-ésimo tren de la estación $i$. En la representación anterior, el máximo representa el hecho de que los trenes no pueden rebasarse unos a otros, por lo tanto, el tren $k$ debe esperar a que el tren $k$ salga de la estación.
Modelado del movimiento de pasajeros
\noindent En particular mostraremos cómo se contabilizan los pasajeros que no logran subir al primer tren. Recordemos que la demanda se modela como procesos de Poisson. Denotaremos por $N_{ik}$ al número de pasajeros
que llegan a la estación $i$ entre las salidas de los trenes $k-1$ y $k$. Si hay suficiente capacidad, todos ellos subirán al tren $k$, pero esto no necesariamente sucede. Entonces los arribos son un proceso de Poisson debido a que se representa como la diferencia entre la demanda actual y la demanda pasada (incrementos). Definimos las siguientes variables:
- $B_{ik}=$ número de pasajeros que viajan en el $k$-ésimo tren entre las estaciones consecutivas $i-1$ e $i$.
- $A_{ik}=$ los que suben.
- $M_{ik}=$ los que bajan.
- $R_{ik}=$ los que se quedan y representan la demanda acumulada para el siguiente tren.
A partir de las definiciones anteriores podemos notar que:
- La demanda potencial $N_{ik}+R_{ik}$
- La capacidad remanente es $K-B_{i-1,k}+M_{ik}$
- Por lo tanto, el número de personas que suben al tren es $$A_{ik}=\min\left(K-B_{i-1,k}+M_{ik},N_{ik}+R_{i,k-1} \right)$$
- Y los que se quedan son $R_{ik}=N_{ik}+R_{i,k-1}-A_{ik}$
Finalmente, si $D_{ijk}$ es el número de pasajeros que toman el tren $k$ en la estación $i$ con destino $j$, entonces la distribución conjunta de los $D_{ijk}$ dado que suben $A_{ik}$ se distribuye multinomial.
La línea 7 del Metro
La línea 7 de la Red de Sistema de Transporte Colectivo de la CDMX tiene una longitud de 18.784 km, de los cuales 17.011 km estan en servicio y el resto se usa para maniobras. Se integra por 14 estaciones, 3 de ellas de correspondencia $($incluida una de sus terminales$)$, 10 de paso y una terminal más; del total, 13 estaciones son subterráneas y una superficial.
| Estación | Afluencia |
| Barranca del Muerto | 3721060 |
| Mixcoac | 2070233 |
| San Antonio | 1372386 |
| San Pedro de los Pinos | 10099776 |
| Tacubaya | 581925 |
| Constituyentes | 753515 |
| Auditorio | 3041596 |
| Polanco | 2988845 |
| San Joaquı́n | 2308943 |
| Tacuba | 727003 |
| Refinerı́a | 913974 |
| Camarones | 1314974 |
| Aquiles Serdan | 1433690 |
| El Rosario | 3320288 |
Cuadro 2: Afluencia de la línea del 7 metro en el periodo Abr-Jun 2017
Simulación
El modelo de simulación se decidió llevar a cabo en la plataforma SIMIO que genera una mejor visualización del problema. El desarrollo de este programa de simulación tiene como objetivo principal probar el funcionamiento de la formulación del sistema. El modelo tiene como entidad a las unidades de metro, mientras contempla como propiedad de la entidad la suma del número de arribos de los usuarios. También simula el movimiento en el sistema del promedio de personas que se encuentran en el tren.
El modelo supone que los tiempos de desplazamiento entre estaciones tienen una distribución exponencial con media 3 en unidades de tiempo $($minutos$)$. El motivo de utilizar esta distribución es debido a la proximidad a la realidad a este tipo de evento, que es el tiempo de servicio de los trenes. Los datos utilizados se obtuvieron de la información disponible del Sistema Colectivo del Metro.
Como se observa en la formulación del problema, se cuenta con 2 distintos procesos de Poisson no homogéneos, uno para describir la llegada de los pasajeros en cada estación y otro de la salida de los pasajeros en cada estación. Los procesos de Poisson de llegada tienen el mismo parámetro de llegada de pasajeros para cada estación, mientras que los procesos de Poisson de salidas tienen un parámetro distinto al de llegadas y menor, idénticos en cada estación.
En cuanto a la generación de tiempos de viaje, llamado con la variable TiempoTotalMetro suponemos que sigue una distribución exponencial con parámetro 3 $($minutos$)$. Debido a que con esta supocisión, podemos observar las filas de espera con Teoría de Colas.
Por otra parte, modelamos el movimiento de pasajeros como una función que cuenta los pasajeros que suben al metro. Para esta condición en cada entrada del servidor, se verifica si la oferta de trenes, definida como 1530 pasajeros menos el número de pasajeros en el tren de una estación atrás es mayor al contador de pasajeros en la estación hasta esa estación más la demanda que desea entrar en esa estación, si se cumple, entonces el contador de pasajeros suma los nuevos pasajeros que entran. $($Nota: tomar en cuenta que la entrada a los vagones está limitada a que deben entrar en bloque generado de pasajeros$)$.
Resultados
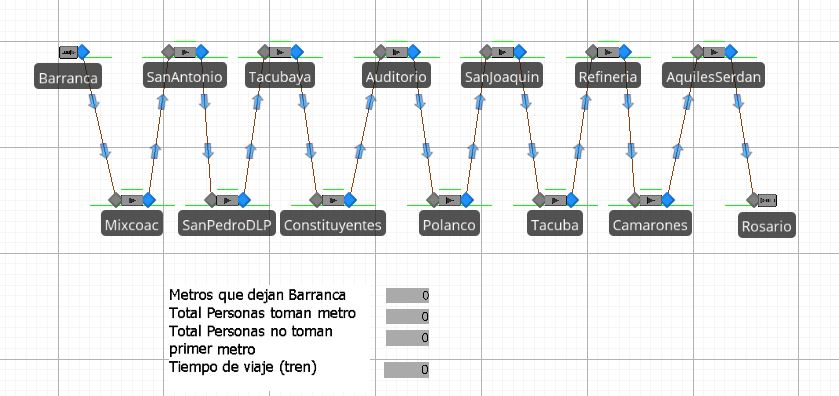
\noindent En lo siguiente se muestran algunas imágenes importantes con los resultados y el modelado del problema en la plataforma SIMIO. En la Figura 1 se puede apreciar la formación del problema, con Entrada en Barranca del Muerto y Salida en Rosario. como se comenta arriba, la distribución de las llegadas entre estaciones conforma una muestra aleatoria. Por lo que puede apreciarse que es un sistema lineal de llegadas y salidas.
En la Figura 2 se pueden observar los resultados de un recorrido del metro por toda la línea, durante 5 horas. Utilizando el día 25 de Julio de 2018 como prueba con los horarios de 6:00 am a 11:00 am. Durante la siguiente imagen, se puede observar parámetros que nos permiten sabes si se acerca nuestra simulación a la realidad. El primer indicador permite saber el número total de trenes que son liberados durante la simulación.
En la Figura 3 podemos observar la validez del constructo de nuestro experimento. Para cada escenario se realizaron 100 repeticiones, generando respuestas para observar cómo se modifica el proyecto.
A continuación se describen 3 escenarios con distintos parámetros:
- FrecuenciaLlegada: es el parámetro del proceso de Poisson para el número de personas que llegan a una estación.
- FrecuenciasSalida: es el parámetro del proceso de Poisson para el número de personas que salen de una estación.
- FrecuenciaTrenes: es el parámetro de la distribución exponencial que describe el número de trenes que salen de la terminal Barranca del Muerto.
\noindent Con las siguientes respuestas de la simulación:
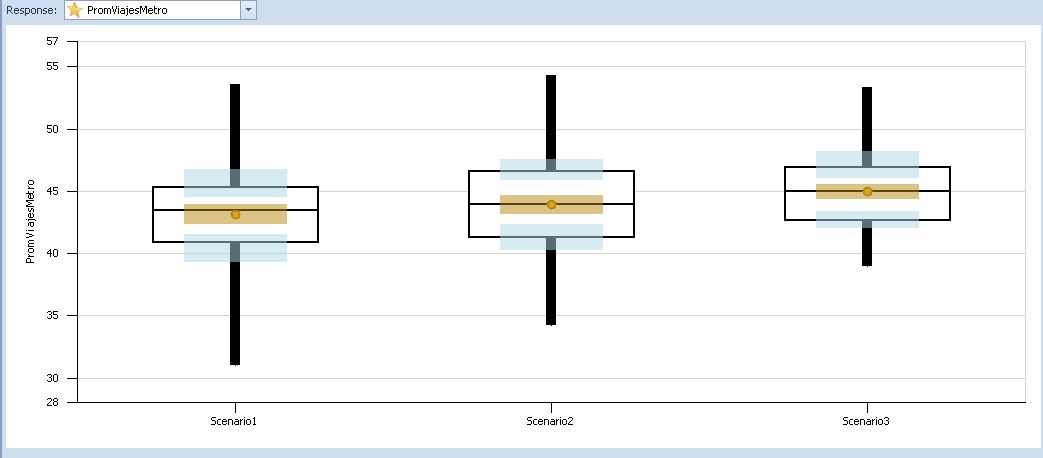
- promViajesMetro: es el promedio del tiempo total del viaje por toda la línea. .
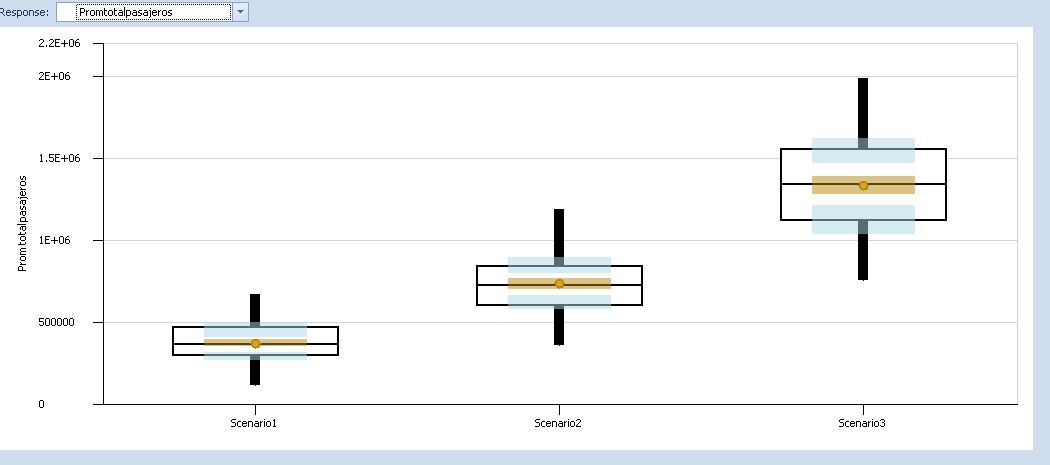
- promTotalPasajeros: es el promedio del total de pasajeros que viajan en la línea.
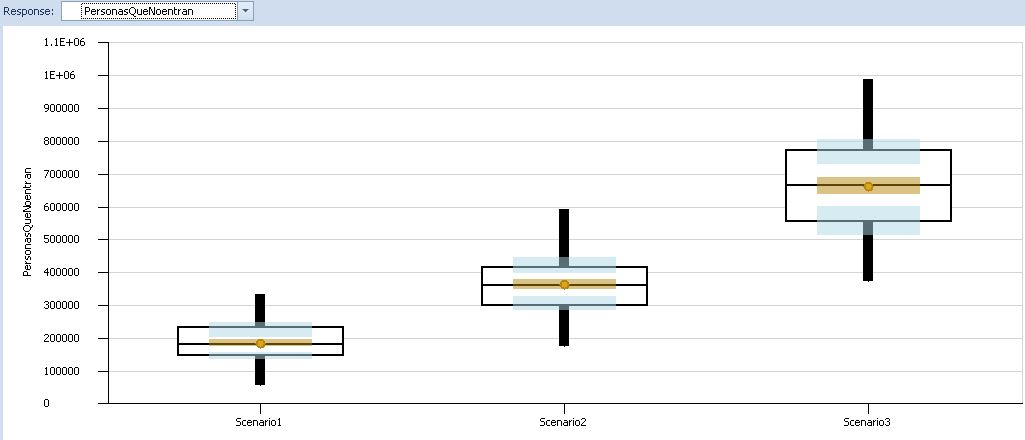
- PersonasQueNoentran: es el promedio del total de personas que no entran en el primer metro que pasa por la estación.
En el Escenario 1, tenemos los siguientes parámetros, en orden, FrecuenciaLlegada=1147, FrecuenciaSalida=802 y FrecuenciaTrenes=20. Por lo que podemos observar que los resultados de las respuestas caen en el rango esperado, esto se observa en las gráficas de brazos. Mientras en el Escenario 2, tenemos los siguientes parámetros, en orden, FrecuenciaLlegada = 1147, FrecuenciaSalida=573 y FrecuenciaTrenes=15. Finalmente en el Escenario 3, tenemos los siguientes parámetros, en orden, FrecuenciaLlegada = 1147, FrecuenciaSalida = 344 y FrecuenciaTrenes = 10.
Por lo que podemos concluir que entre menor sea la frecuencia de Trenes será mayor el total de personas que no podrán entrar en el primer tren que pase, teniendo que esperar al siguiente y aumentando el tiempo de espera. También podemos observar que entre mayor sea la Frecuencia de Salida del usuario en la estación, menor tendrá que esperar. Sin embargo, esta variable no es posible controlarla como podría ser la Frecuencia de Trenes en el sistema logístico de decisiones del Sistema Colectivo del Metro.
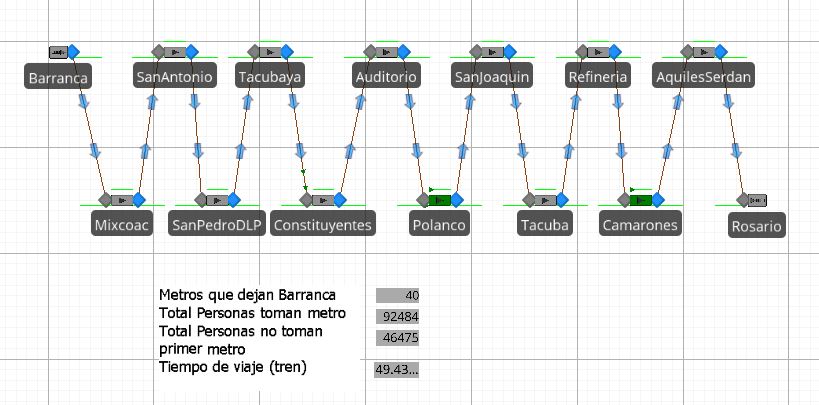
Figura 2: Interfaz de Programa SIMIO cuando se realiza el primer recorrido del metro durante 5 horas

Figura 3: Resultados del experimento de 100 repeticiones, cambiando los parámetros de las llegadas y salidas de pasajeros
1Acero, Juan Camilo & Riaño, Germán. «Implementación y análisis de un modelo estocástico de despacho de vehículos de trasnporte masivo’’, Revista de Ingeniería: Facultad de Ingeniería, Universidad de los Andes 21 (2005):6-18 pp.,2
Billingsley, Patrick. Probability and Measure, 3ed. John Wiley & Sons, 1975.,3 Karlin, Samuel & Taylor, Howard M. A First Course in Stochastic Processes. Academic Press, 1995.,4 «Datos y estadísticas de uso del transporte público en Ciudad de Mexico, México’’ Moovit Insights. Consultado el 24 de Julio de 2018 https://moovitapp.com/insights/es,5
«Afluencia de estación por línea 2017’’ Sistema de Transporte Colectivo, Consultado el 24 de Julio de 2018 http://www.metro.cdmx.gob.mx.
Bibliografia
| 1. | ↑ | Acero, Juan Camilo & Riaño, Germán. «Implementación y análisis de un modelo estocástico de despacho de vehículos de trasnporte masivo’’, Revista de Ingeniería: Facultad de Ingeniería, Universidad de los Andes 21 (2005):6-18 pp. |
| 2. | ↑ | Billingsley, Patrick. Probability and Measure, 3ed. John Wiley & Sons, 1975. |
| 3. | ↑ | Karlin, Samuel & Taylor, Howard M. A First Course in Stochastic Processes. Academic Press, 1995. |
| 4. | ↑ | «Datos y estadísticas de uso del transporte público en Ciudad de Mexico, México’’ Moovit Insights. Consultado el 24 de Julio de 2018 https://moovitapp.com/insights/es |
| 5. | ↑ | «Afluencia de estación por línea 2017’’ Sistema de Transporte Colectivo, Consultado el 24 de Julio de 2018 http://www.metro.cdmx.gob.mx. |