Introducción a la Teoría de Floquet en dos dimensiones

Introducción

En el ámbito de Ecuaciones Diferenciales Ordinarias, el problema arquetipo de un sistema n-dimensional es dado por

\begin{align*}
\dot{x}=Ax,
\end{align*}

donde $A$ es una matriz cuadrada con coeficientes constantes y reales de dimensión $n\times{n}$. Describir las soluciones de ese problema se reduce a saber cómo se comporta la matriz $A$, pero ¿qué pasa si sus coeficientes ya no son constantes? Es decir

\begin{align*}
(A)_{i,j}=f_{i,j}(t),
\end{align*}

donde $f_{i,j}$ es una función de $\mathbb{R}$ a $\mathbb{R}$ para todo $i,\,j\,=\{1,\cdots,n\}$. Luego, el sistema se deja escribir de la siguiente forma:

$$\dot{x}=A(t)x\quad\quad(1)$$

El problema de arriba se ve bastante interesante, pero encontrar su solución será más difícil debido a que es un problema más robusto. Por esto consideremos una particularidad del problema anterior.

Sea el sistema n-dimensional dado por
$$\dot{x}=P(t)x,\quad\quad(2)$$

donde $P(t)$ es una matriz cuadrada cuya dimensión es de $n\times{n}$ y es tal que sus coeficientes son periódicos con periodo mínimo $T$. Es decir, $P(t)$ y $T$ son tales que

$$P(t+T)=P(T),\quad-\infty<t<\infty.\quad\quad(3)$$.

«Estos sistemas pueden surgir del mundo real, por ejemplo, cuando un sistema mecánico tiene un forzamiento periódico o es el sistema linealizado de un orbital T-periódico» ¹James D. Meiss.DifferentialDynamicalSystems. Monographs on Mathematical Mode-ling and Computation. Society for Industrial and Applied Mathematics, 2007..

Una primera idea es que las soluciones del sistema también son periódicas. Es decir, las condiciones iniciales regresen a sus valores originales después de un tiempo $T$. Esto es equivalente a que la matriz de mondromía, la cual se encuentra más adelante.} $M$ es tal que $M(t_0)=\mathbb{I}$, donde $\mathbb{I}$ denota a la matriz identidad.

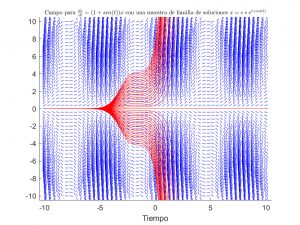
Figura 1: Las líneas azules son el campo vectorial de $\dot{x}=(1+\sin(t))x$, el cual tiene una estructura periódica. Las lineas rojas son muestras de la solución general $x^*=c\exp(t-\cos(t))$ tomando $c=-20,\dots,20$

Esta idea es errónea; no es necesario salir de un sistema de una dimensión para hallar un contra-ejemplo como el de la Figura 1. Sea el sistema $\dot{x}=(1+\sin(t))x$, este claramente es $2\pi$-periódico; sin embargo, su solución en general no lo es; la solución del sistema es $x^*=c\exp(t-\cos(t))$, con $c$ una constante real, la cual es periódica si y solo si $c=0$.
\newline

Achille Marie Gaston Floquet$($1847-1920$)$, mejor conocido como Gaston Floquet fue un matemático francés que enunció el teorema que hoy es conocido de Floquet y desarrolló la teoría ahora conocida como de Floquet. Ambos resultados caracterizan las soluciones de los problemas de la forma $\dot{x}=P(t)x$ . Estos resultados se presentan en sus publicaciones divididas en tres artículos con el nombre Sur les équations différentielles linéaires à coefficients périodiques $($dos publicados en 1881 y uno en 1883$)$, Sur les équations différentielles linéaires à coefficients doublement périodiques $($1884$)$ y su tesis doctoral Sur la théorie des équations différentielles linéaires $($1879$)$ la cual ya presentaba las ideas que posteriormente desarrolló en sus publicaciones posteriores.

Teoría de Floquet

Consideremos el problema de valores iniciales (PVI) dado por el sistema $($2$)$ con $P$ que satisfaga $($3$)$ y el valor inicial $x(t_0)=x_0$. Esto es, consideramos el PVI de la forma
$$\left.\begin{matrix}
\dot{x}=P(t)x,\\
x(t_0) =x_0.
\end{matrix}\quad\right\}\quad\quad(4)$$
con $T$ un valor real tal que $P(t+T) = P(t)$; $P$ es $T$-periódica.

A pesar de que la idea de valores iniciales con comportamiento periódico es en general errónea, es una idea interesante pues el sistema induce al hecho de que una solución $x^*$ es $T$-periódica. Estudiar esta familia de soluciones puede ser bastante complicado, pero sabemos que las soluciones están caracterizadas por la matriz fundamental. Esta estructura nos permitirá estudiar el comportamiento de todas las soluciones con una notación fácil; se seguirá la notación de Meiss por costumbre.D

Definicion 1: $($Matriz de Mondromía$)$: Dado un sistema de la forma $($4$)$, se sabe por el teorema de unicidad y existencia de soluciones que existe la matriz fundamental, $\Phi(t,t_0)$. Entonces, se define la matriz de mondromía $M(t_0)$ como $M(t_0)=\Phi(t_0,t_0)^{-1}\Phi(T,t_0)$. Si se define a $\Phi(t_0,t_0)=\mathbb{I}$ usando la matriz fundamental principal, entonces $M(t_0)$ será la matriz fundamental principal evaluada en un periodo.

Lema: $($Invarianza en el tiempo$)$: La matriz de mondromía es independiente del tiempo, es tal que $\Phi(t_0+lT,t_0)=M^l(t_0)$ con $l$ un número entero y además es invariante ante cambios en el valor $t_0$.

Demostración: La primera parte se cumple por definición de $M$.
La invarianza sobre el valor de $t_0$ se obtiene por la unicidad de la solución; esto implica que la matriz fundamental satisface $\Phi(t,r)=\Phi(t,s)\Phi(s,r)$, entonces
$$ M(t_1)=M(t_0)\Phi(t_0,t_1).$$
Por eso, de ahora en adelante denotaremos a $M(t_0)=M$.
Dado que $x(t)=\Phi(t,t0)x_0$, entonces $x(T)=\Phi(T,t_0)x_0=Mx_0$. Luego, por un argumento de inducción sobre $l$ y definiendo la nueva variable $\tau=t-T$, se tiene el PVI
\begin{equation*}
\dot{x}=A(\tau)x,\quad x(t_0)=M^lx_0,
\end{equation*}
cuya solución es $\Phi(\tau,0)M^lx_0=M^{l+1}x_0.$

$\square$

El lema anterior nos da a entender que nuestra primera idea de soluciones no estaba alejada de la realidad; solo necesitaba retoques. Además, nos apunta a que las soluciones están establecidas por los valores propios de $M$; si es que existen y no son cero.

Lema $($No singularidad$)$: La matriz de mondromía es no singular.

Demostracion: $\det(M)=\det(\Phi(T,t_0))\not=0$, por ser la matriz fundamental principal.

$\square$

Definicion 2: $($Multiplicadores de Floquet, exponentes de Floquet$)$. Los valores propios de la matriz $M$, denotados como $\rho_i$, son definidos como los multiplicadores de Floquet y al valor $\mu_i$ tal que $\rho_i=\exp\{\mu_iT\}$ se le llama exponente de Floquet.

Es necesario notar que los multiplicadores de Floquet pueden ser complejos, lo cual hace que se deba considerar a la función $\exp\{\cdot\}$ en su versión compleja. En consecuencia, los exponentes de Floquet no son únicos pues son $2\pi i$-periódicos.
Adicionalmente, los multiplicadores de Floquet son intrínsecos a la forma del sistema y no dependen de la elección de $\Phi(t)$. Si se tienen dos matrices fundamentales, digamos $\Phi_1$ y $\Phi_2$, entonces siempre existe una matriz constante no singular, $C$, tal que $\Phi_1=\Phi_2C$.

Lema $($Determinante de la matriz de Mondromía$)$. $\det{M}=\exp\{\int_0^{T}\text{tr}(A(s)){ds}\}$.

Demostración: De la identidad de Abel-Jacobi-Liouville se tiene que si la traza de $A$ es una función continua; entonces,
\begin{equation*}
\det(M)=\det(\Phi(T,t_0))=\det(\Phi(t_0,t_0))\exp\left\{\int_{t_0}^{t_0+T}\text{tr}(A(s)){ds}\right\}=\exp\left\{\int_{0}^{T}\text{tr}(A(s)){ds}\right\}.
\end{equation*}

$\square$

El lema anterior nos indica una vez más que la matriz $M$ no depende del tiempo, ni de la elección de $t_0$. Adicionalmente, se tiene que $\det(M)=\Pi_{i=1}^n\rho_i$.

Teorema 1 $($Floquet 1883$)$. Sea $M$ la matriz de mondromía del sistema $($4$)$ y $TB=\ln\{M\}$, donde la función $\ln\{\cdot\}$, puede ser en sus versión compleja y de serlo se toma la rama principal. Entonces, existe una matriz $T$-periódica $P$ tal que la matriz fundamental del sistema se deja expresar como $$\Phi(t,t_0)=P(t)\exp\{tB\}\quad\quad(5)$$
y $P(t_0,t_0)=\mathbb{I}$, la matriz identidad de la dimensión correspondiente. A la ecuación $($5$)$ se le conoce como la Forma Normal de Floquet de la matriz fundamental.

Demostración: Sea $\Psi(t)=\Phi(t+T,t_0)$, como $A$ es periódica, entonces $\dfrac{d}{dt}\Psi=A(t+T)\Psi=A(t)\Psi$ y $\Psi(t_0)=M$.

Como $\Phi$ es la matriz fundamental de soluciones se tiene que toda solución $x(t)$ es de la forma $x(t)=\Phi(t,t_0)x(t_0)$. Luego, $\Psi(t)=\Phi(t,t_0)M$ y por lo tanto $\Phi(t+T,t_0)=\Phi(t,t_0)M=\Phi(t,t_0)\exp\{TB\}$.

Luego, con $P(t)\equiv\Phi(t,t_0)\exp\{-tB\}$ se demuestra el teorema. Pues
\begin{equation*}
P(t+T)=\Phi(t+T,t_0)\exp(-(t+T)B)=\Phi(t,t_0)\exp(TB)\exp(-(t+T)B)=P(t).
\end{equation*}
Lo cual termina la demostración pues se encontró la solución y satisface la condición de periodicidad.

$\square$

Corolario. Existe una matriz $2T$-periódica $Q$ y una matriz $R$, ambas reales tales que $\Phi(t,t_0)=Q(t)\exp\{tR\}$.

Demostración: El álgebra lineal nos dice que para toda matriz $M$ no singular, existe $R$ una matriz real tal que $M^2=\exp\{TR\}$. Luego, sea $Q(t)=\Phi(t,t_0)\exp\{-tR\}$ y satisface
\begin{equation*}
Q(t+2T)=\Phi(t+2T,t_0)\exp\{-2TR\}\exp\{-tR\}=\Phi(t,t_0)M^2M^{-2}\exp\{-tR\}=Q(t)
\end{equation*}

$\square$

Observamos que el corolario da una caracterización real de las soluciones. Luego, el cambio de variable $y=Q^{-1}(t)x$ nos da un sistema dependiente del tiempo de la forma
\begin{align*}
\left\{\begin{matrix}
\dot{y}=Ry,\\
y(t_0)=Q^{-1}(t_0)x_0.
\end{matrix}\right.
\end{align*}
Mientras que el teorema nos da el cambio de variable $y=P^{-1}(t)x$ que a su vez nos da el sistema
\begin{align*}
\left\{\begin{matrix}
\dot{y}=By,\\
y(t_0)=P^{-1}(t_0)x_0.
\end{matrix}\right.
\end{align*}

Consideremos el siguiente ejemplo: Sea $x=(x_1,x_2)^T$ y ahora consideremos el sistema \begin{equation*}
\dot{x}=\begin{pmatrix}
\left(1+\dfrac{\cos(t)}{2+\sin(t)}\right) & 0 \\
1 & -1
\end{pmatrix}x.
\end{equation*}

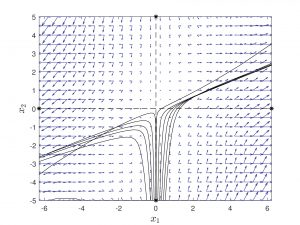
Figura 2: Las lineas azules son el campo vectorial del sistema y trazas negras son muestras de las soluciones.

La solución general es dada por, $x=c_1e^t\begin{pmatrix}2+\sin(t)\\2+.5\sin(t)-.5\cos(t)\end{pmatrix}+c_2e^{-t}\begin{pmatrix}0 \\ 1\end{pmatrix}$, con $c_1,c_2$ constantes reales.

Sea la matriz fundamental
$\Phi(t)=\begin{pmatrix}
e^t(2+\sin(t)) & 0 \\e^t(2+.5\sin(t)-.5\cos(t)) & e^{-t}
\end{pmatrix}$, debido a las funciones seno y coseno esta matriz es $2\pi$-periódica.
Entonces,
\begin{align*}
M&=\Phi^{-1}(0)\Phi(2\pi)
&=\begin{pmatrix}1 & 0\\\dfrac{-3}{2} & 2
\end{pmatrix}\begin{pmatrix}2e^{2\pi} & 0\\ \dfrac{3}{2}e^{2\pi} & e^{-2\pi}\end{pmatrix}
\end{align*} por lo tanto $
M=2\begin{pmatrix}e^{2\pi} & 0\\ 0 & e^{-2\pi}\end{pmatrix}$.
Se deduce que $\rho_1=e^{2\pi}$ y $\rho_2=e^{-2\pi}$; consecuentemente $\mu_1=1$ y $\mu_2=-1$ y por lo tanto, $P(t)\equiv\Phi(t)$.
Luego, es equivalente estudiar el sistema $\dot{y}=2\begin{pmatrix}e^{2\pi} & 0\\ 0 & e^{-2\pi}\end{pmatrix}y$.

Estabilidad para sistemas de dos dimensiones

Note que $x_j(t)=e^{t\mu_j}p(t)$ es una solución. De hecho, es la j-ésima entrada de caracterización de la matriz fundamental dada por Floquet. Recordando el lema ??, tenemos que $x_j(t+NT)=\rho^Nx(t)$,
\begin{lemma}(Estabilidad)
Cada multiplicador de Floquet satisface solo una de las siguientes condiciones:

1. Si $|\rho|<1$, entonces $\Re(\mu)<0$ y por lo tanto $x\underset{t->\infty}{\longrightarrow}0$.
2. Si $|\rho|=1$, entonces $\Re(\mu)=0$ y por lo tanto existen orbitales pseudo-periódicas. Además, si $\rho=\pm1$ entonces son órbitas $T$-periódicas.
3. Si $|\rho|>1$, entonces $\Re(\mu)>0$ y por lo tanto $x\underset{t->\infty}{\longrightarrow}\infty$.
4. Si $\forall{j}\,|\rho_j|\leq1$ se dice que la solución entera es estable.

Adicionalmente, se pueden demostrar varios criterios de estabilidad dependiendo de dónde surge el sistema. Es de particular interés estudiar la estabilidad de ecuaciones con la forma
\begin{align*}
\ddot{x}+a(t)x=0,
\end{align*}
con $a(t)$ $T$-periódica. Se sigue del estudio en ²University of British Columbia. Basic Floquet Theory.http://www.math.ubc.ca/~ward/teaching/m605/every2_floquet1.pdf. que la ecuación se puede expresar en el sistema
\begin{align*}
\begin{pmatrix} x’_1 \\ x’_2\end{pmatrix}=\begin{pmatrix}
0 & 1 \\ -a(t) & 0 \end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}.
\end{align*}
Tomando la condición inicial $(x_1(0),x_2(0))^T=(1,0)^T$ tenemos una solución de la forma $(x^{(1)}(t),x^{‘(1)}(t))^T$, análogamente con $(x_1(0),x_2(0))^T=(0,1)^T$. Para llegar a la matriz fundamental
\begin{align*}
\Phi(t,0)=\begin{pmatrix}
x^{(1)}(t) & x^{(2)}(t)\\x^{‘(1)}(t) & x^{‘(2)}(t)
\end{pmatrix},
\end{align*}
para poder concluir
\begin{align*}
M=\begin{pmatrix}
x^{(1)}(T) & x^{(2)}(T)\\x^{‘(1)}(T) & x^{‘(2)}(T)
\end{pmatrix}.
\end{align*}
Ahora, por el lema ??. $\det(M)=\rho_1\rho_2=\int_0^T\text{tr}(A(s))ds$, pero $\int_0^T\text{tr}(A(s))ds=\int_0^T0ds$ y por el hecho de que $\rho_1+\rho_2=\text{tr}(M)$ se tiene que
\begin{align}\label{ro}
\rho_1\rho_2=1\\
\rho_1+\rho_2=x^{(1)}(T)+x^{‘(2)}(T).
\end{align}
Sea $2\upsilon=\text{tra}(B)$ y resolviendo el sistema de ecuaciones se tiene que
\begin{align}
\rho=\upsilon\pm\sqrt{\upsilon^2-1}.
\end{align}
Recordamos que $\rho$ es un multiplicador de Floquet, por lo tanto existe su exponente de Floquet asociada. Sustituyendo $\rho=\exp\{T\mu\}$ tenemos que,
\begin{align}
\mu_1+\mu_2=0
\end{align}
luego
\begin{align}
\upsilon=\dfrac{\exp\{T\mu_1\}+\exp\{T\mu_2\}}{2}=\dfrac{\exp\{T\mu_1\}+\exp\{-T\mu_1\}}{2}=\cosh(T\mu_1).
\end{align}
Haciendo el estudio de casos y usando los cambios de variables que inducen el teorema y el corolario tenemos el siguiente resultado:

1. Si $\upsilon>1$, las soluciones son inestables de la forma \begin{align}
   x(t)=c_1\exp\{t\mu_1\}p_1(t)+c_2\exp\{-t\mu_2\}p_2(t).
   \end{align}
2. Si $\upsilon=1$, las soluciones son inestables de la forma \begin{align}
   x(t)=(c_1+tc_2)p_1(t)+c_2p_2(t).
   \end{align}
3. Si $\upsilon\in(-1,1)$, las soluciones son estables pseudo-periódicas de la siguiente forma \begin{align}
   x(t)=c_1\Re(\exp\{it\sigma\}p_1(t))+c_2\Im(\exp\{it\sigma\}p_2(t)),
   \end{align}
   con $\sigma=\dfrac{2\pi}{nT}$ con $n>2$.
4. Si $\upsilon=-1$, las soluciones son inestables de la forma \begin{align}
   x(t)=(c_1+tc_2)q_1(t)+c_2q_2(t).
   \end{align}
5. Si $\upsilon<-1$, las soluciones son inestables de la forma \begin{align}
   x(t)=c_1\exp\{t\gamma\}q_1(t))+c_2\exp\{t\gamma\}q_2(t)),
   \end{align}
   con $\gamma=\mu_1-\dfrac{i\pi}{T}$.