Activa tus neuronas

Retos matemáticos

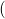$($ Putman Exam 2010) Encuentra todas las funciones diferenciables 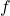$f$ tales que
$f'(x)=\frac{f(x+n)-f(x)}{n},\qquad \forall x \in\mathbb{R}, \forall n \in\mathbb{N}$
(RESPUESTA)
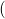Putnam Exam 2010) Sea 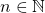fija. ¿Cuál es la 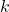más grande tal que el conjunto admite una partición de 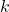subconjuntos 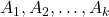de tal forma que se cumple
$\sum A_i = \sum A_j$
para cualquier par ?
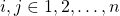- Recordatorio: Para un conjunto 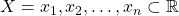$X={x_1,x_2,\ldots,x_n}\subset \mathbb{R}$ , se define 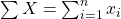$\sum X = \sum_{i=1}^n x_i$ (la suma de todos los elementos de 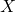$X$ ). (RESPUESTA)
Encuentre todos los valores de 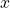$x$ para los que se cumple
$x+2{x} = 3[x]$
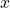donde ${x}$ representa la parte fraccionaria de 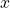$x$ y $[x]$ , la parte entera.(RESPUESTA)
Sea 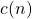${c(n)}$ una sucesión donde $c(1) = 1$

$c(2n)= c(n)$

$c(2n+1)= (-1)^n c(n).$
Encuentra el valor de
$\sum_{n=1}^{2020} c(n)c(n+2)$
(RESPUESTA)

Enigmas matemáticos

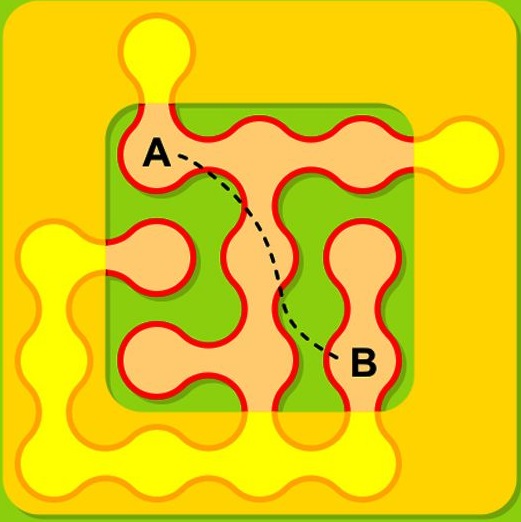
¿ADENTRO O AFUERA?

En la siguiente ilustración se muestra una curva cerrada simple muy sinuosa y una parte de ella se encuentra escondida debajo de una hoja de papel con un hueco en medio. Si te dijeramos que la región $\mathbf{A}$ se encuentra dentro de la curva, entonces la región $\mathbf{B}$ , ¿está dentro o afuera? (RESPUESTA)

NO ES LO QUE PARECE

Esto puede parecer contradictorio en sí mismo, pero encuentra tres números enteros en progresión aritmética $($ es decir, la resta entre dos números consecutivos de la serie es siempre la misma) cuyo producto sea un número primo.(RESPUESTA)

¡FELIZ CUMPLEAÑOS!

Supón que estás celebrando tu cumpleaños número $30$ y tus amigos han decidido comprarte un pastel con $30$ velas encendidas para comer a la hora del postre. Es momento de apagar las velitas, después de haberte cantado las Mañanitas o el Happy Birthday. Sin embargo, cada vez que soplas solamente logras apagar un número aleatorio de velas entre $1$ y el resto de velas que aun esta encendidas. ¿Cuántas veces deberás soplar, en promedio, para apagar todas las velas?(RESPUESTA)

Respuestas

Retos matemáticos

Pregunta 1

Para los primeros dos valores de $n\in \mathbb{N}$ se tiene que:

$f'(x) &= \frac{f(x+1)-f(x)}{1} = f(x+1)-f(x)\label{eq:1.1}$

$f'(x) &= \frac{f(x+2)-f(x)}{2}\label{eq:1.2}$

En $n=2$ sumamos y restamos el término $f(x+1)$ y reordenamos para incluir la expresión $n=1$ , es decir,

$f'(x) = \frac{[f(x+2)-f(x+1)] + [f(x+1)-f(x)] }{2}$

$f'(x) = \frac{1}{2}(f((x+1)+1)-f(x+1)) + \frac{1}{2}(f(x+1-f(x))\$

$f'(x) = \frac{1}{2}f'(x+1) + \frac{1}{2}f'(x)$

A partir de esto se deduce que

$f'(x+1)=f'(x), \qquad \forall x\in\mathbb{R}$

Por lo tanto,

$f'(x+1) - f'(x) = 0$

$\implies\quad \frac{d}{dx}\left(f(x+1)-f(x)\right) = 0$

$\implies\quad f(x+1) -f(x) = c \quad \text{para alguna constante }c\in\mathbb{R}$

$\implies\quad f'(x) = c \quad \text{por el caso } n=1$

$\implies \quad f(x) = cx + d \quad \text{para alguna constante }d\in\mathbb{R}$

Por lo que las funciones que satisfacen la condición son las funciones lineales de la forma $f(x) = cx+d$ con $c,d\in\mathbb{R}$ .

Pregunta 2

Comencemos con algunos ejemplos.

Para 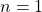$n=1$ : el conjunto 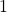${1}$ admite solo una partición. Entonces, $k=1$ .
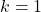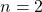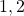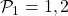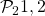Para $n=2$ : el conjunto ${1,2}$ admite las particiones $\mathcal{P}_1 = {{1},{2}}$ y $\mathcal{P}_2{{1,2}}$ . Es fácil verificar que 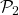$\mathcal{P}_2$ no satisface la condición, pero 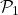$\mathcal{P}_1$ , sí. Entonces $k=2$ .
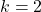Para 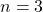$n=3$ : la única partición que satisface la condición es 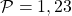$\mathcal{P}={{1,2}{3}}$ . Entonces,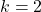 $k=2$

Podemos seguir desarrollando algunos casos para $n>3$ , sin embargo, se puede notar que hay un patrón relacionado con la paridad de $n$ .
Si $n=2m$ , entonces $k=m$ .
Si $n=2m+1$ , entonces $k=m+1$ .

Pregunta 3

Notemos que para cualquier $x\in\mathbb{R}$ se tiene que

$x = [x]+{x}$

con $[x]\in\mathbb{Z}$ y ${x}\in[0,1)$ . Entonces,

$x+2{x} = 3[x]$

$\iff \quad ([x]+{x})+2{x} = 3[x]$

$\iff \quad [x] = \frac{3}{2}{x}$

$\iff \quad [x] \in [0,3/2)$

$\iff \quad \begin{cases} [x]=1 \text{ ó } [x]=1$

Si $[x]=0$ , entonces ${x}=0$ y, por lo tanto, $x=0$ . Si $[x]=1$ , entonces ${x}=2/3$ y, por lo tanto, $x=1+2/3= 5/3$ .

Pregunta 4

https://www.youtube.com/watch?v=5kwdrI89SI8

Enigmas matemáticos

¿ADENTRO O AFUERA?

Relacionado con el Teorema de Jordan y bajo el contexto de una curva simple cerrada $\mathcal{L}$ , si la línea que se traza entre dos puntos intersecta un número par de veces a la curva $\mathcal{L}$ entonces ambos puntos se encuentran, al mismo tiempo, dentro o fuera de la región: si es impar, uno de ellos se encontrará fuera y otro dentro. Por lo tanto, resulta que la región región $\mathbf{B}$ está dentro.

NO ES LO QUE PARECE

Los enteros son $-3,-1,1$ .

¡FELIZ CUMPLEAÑOS!

Notemos que al tener $n$ velas entonces nos puede tomar, a lo más, $n$ soplos para apagarlas todas. Si tuviéramos $n=1$ vela, entonces nos tomaría un soplido. Si tuviésemos $n=2$ velas, la mitad de las veces las apagaríamos todas de un solo soplido y la otra mitad nos tomaría 2. Para $n=3$ velas, la tercera parte de las veces nos tomaría 1 soplido $($ apagarlas todas); la otra tercera parte implica que primero apagamos 1 y nos restan 2, es decir, nos tomaría el promedio de solo tener 2 más un soplido; y, finalmente, tenemos que nos tomaría 2 soplidos si apagáramos todas excepto una $($ al primer soplido). Lo anterior se resume en la siguiente lista.

$p_1 = \text{1 Vela} = 1$
$p_2 = \text{2 Velas} = \frac{1}{2}(1) + \frac{1}{2}\Big(1+\underbrace{1}_{p_1}\Big) = 1 + \frac{1}{2}$
$p_3 = \text{3 Velas} = \frac{1}{3}(1) + \frac{1}{3} \Big( 1 + \underbrace{1 + \frac{1}{2}}<em>{p_2} \Big) + \frac{1}{3}\Big(1+\underbrace{1}</em>{p_1}\Big) = 1 + \frac{1}{2} + \frac{1}{3}$
$p_4 = \text{4 Velas} = \frac{1}{4}(1) + \frac{1}{4} \Big( 1 + \underbrace{1 + \frac{1}{2} + \frac{1}{3}}<em>{p_3} \Big) + \frac{1}{4}\Big( 1 + \underbrace{1 + \frac{1}{2}}</em>{p_2} \Big)+ \frac{1}{4}\Big(1+\underbrace{1}_{p_1}\Big) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}$
$\vdots$
$p_k = k\text{ Velas} = \frac{1}{k}(1) + \frac{1}{k}(1+p_{k-1}) + \frac{1}{k}(1+ p_{k-2}) +\cdots + \frac{1}{k}(1+p_1)$
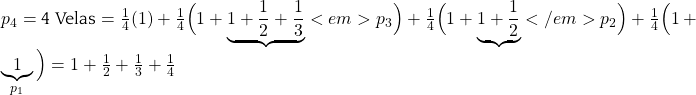
$= 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{k} = \sum_{i=1}^k \frac{1}{i}.$