La meta y la motivación para llegar a ella
A la hora de realizar el estudio numérico de una función por medio de la técnica de interpolación polinomial, es natural preguntarse por la precisión de nuestra aproximación en determinado intervalo de la recta real. Aunque es difícil precisar algo de esta naturaleza para una función en general, dados una cantidad finita de puntos y una función con características particulares, el siguiente resultado y meta de esta monografía nos da un parámetro analítico para juzgar al error al que podríamos incurrir de manera numérica.
Proposición 1: Dados $f$, una función perteneciente al espacio $C^{n+1}\left([a,b]\right)$, y $p_n(f;x)$, el polinomio que interpola a la función en $n+1$ puntos, si los nodos son tales que $a$ ≤ $x_0$ < $x_1$ < $…$ < $x_n$ ≤ $b$, entonces existe $\xi$ en $(a,b)$ de manera que
$f(x)-p_n(f;x)=\dfrac{(x-x_0)(x-x_1)…(x-x_n)}{(n+1)!}f^{(n+1)}(\xi)$.
El lector que haya cursado cálculo podrá intuir el fluir de la demostración de este teorema dado sus hipótesis. Hagamos esto con lujo de detalle.
Una proposición y dos corolarios del cálculo básico
En esta sección$($y, en realidad, en lo que resta del texto salvo en contadas excepciones$)$ seguiremos muy de cerca los enunciados y demostraciones que se pueden encontrar en la página 107 de Principles of Mathematical Analysis, de Walter Rudin y página 57 de Interpolation and Approximation, de Philip J. Davis.
Proposición 2: Sean $f$ y $g$ funciones reales continuas en el intervalo cerrado $[a,b]$ y diferenciables en el abierto $(a,b)$, entonces
\begin{equation}
[f(b)-f(a)]g'(\xi)=[g(b)-g(a)]f'(\xi)
\end{equation} para algún $\xi$ en $(a,b)$.
Demostración: Definamos $h:(a,b)\to\mathbf{R}$ con regla de correspondencia $h(t)=[f(b)-f(a)]g(t)-[g(b)-g(a)]f(t)$. Notemos que $h$ es continua y diferenciable, ya que es la suma de dos funciones continuas y diferenciables. Además, es el caso que $h(a)=f(b)g(a)-f(a)g(b)=h(b)$, por lo tanto, $h'(\xi)=0$, cuando menos, para un $\xi$ en $(a,b)$, siguiéndose directamente la ecuación en la proposición 2.
$\square$
Ahora, si en la ecuación tomamos $g(x)=x$, entonces tenemos la siguiente proposición universalmente conocida como el teorema de Rolle,
Proposición 3: Sea $f$ una función continua en el intervalo cerrado $[a,b]$ y diferenciable en el abierto $(a,b)$. Si $f(a)=f(b)$, entonces existe un punto $\xi$ en $(a,b)$ tal que $f'(\xi)=0$.
Una extensión natural de nuestro pensamiento respecto a los teoremas pasados sería la de preguntarnos cuáles son las condiciones necesarias para asegurar la existencia de un cero en la derivada de orden enésimo de una función. Convenientemente, este resulta ser el paso crucial para realizar la demostración de nuestra meta.
Proposición 4: Sean $n\geq2$ y $f$ una función en $C^n [a,b]$. Si es el caso que existen $x_0,x_1,…,x_n$ tales que para cualquier $j\in\{0,1,2,…,n \}, f(x_j)=0$ y $a\leq x_o<x_1<…<x_n\leq b$, entonces existen un real $\xi$ en $(x_0,x_n)$ tal que $f^n(\xi)=0$.
Demostración: Notemos que $a\leq x_o<x_1<…<x_n\leq b$ y que para cualquier $j\in\{0,1,2,…,n \}$ es el caso que $f(x_j)=0$, así que, por el teorema de Rolle, tenemos que existen $\xi_{1_k}$ con $k$ entre $0$ y $n-1$ tales que $x_o<\xi_{1_0}<x_1<\xi_{1_1}<x_2…<x_{n-1}<\xi_{1_{n-1}}<x_n$ y $f'(\xi_{1_k})=0$. De esta manera, observemos que las hipótesis del teorema de Rolle surgen cada vez que lo volvemos a utilizar, así, gracias a la enésima aplicación del teorema, existe $\xi$ en $(x_0,x_n)$ tal que $f^{(n)}(\xi)=0$.
$\square$
La demostración del teorema
Demostración: Como $p_n(f;x)$, por definición, interpola a f, entonces $p_n(f;x_k)=f(x_k)$, lo cual implica que la función $f(x)-p_n(f;x)$ es igual a cero para cualquier $x_k$. Ahora, fijemos a $x$ de manera que sea distinta a $x_0, x_1,…, x_{n-1}$ y $x_n$ y definamos a la siguiente función en términos de $t$
\begin{equation}
W(t)=f(t)-p_n(f;t)-\frac{f(x)-p_n(f;x)}{\prod_{j=0}^{n}(x-x_j)}\prod_{j=0}^{n}(t-x_{j}).
\end{equation}
De aquí se desprenden algunas consecuencias: en primera instancia, $W(t)=0$ cuando $t=x_0,t=x_1,…,t=x_n$, pero no sólo ahí, la construcción de $W$ nos asegura que $W(x)=0$. En segundo lugar, y considerando lo anterior aunado a la cuarta proposición, existe un punto $\xi$ en el intervalo $(min\{ x,x_0,…,x_n\},max\{ x,x_0,…,x_n\})$ de manera que $W^{n+1}(\xi)=0$, pero
\begin{equation*}
W^{n+1}(t)=f^{n+1}(t)-(n+1)!\frac{f(x)-p_n(f;x)}{\prod_{j=0}^{n}(x-x_j)},
\end{equation*}
de manera que obtenemos que
\begin{equation}
\frac{f(x)-p_n(f;x)}{\prod_{j=0}^{n}(x-x_j)}=\frac{f^{n+1}(\xi)}{(n+1)!} .
\end{equation}
Insertando esto ultimo en la primera ecuación, concluimos que para algún $\xi$ en $(a,b)$ se cumple que
$ f(x)-p_n(f;x)=\dfrac{(x-x_0)(x-x_1)…(x-x_n)}{(n+1)!}f^{(n+1)}(\xi)$.
$\square$
Un poco de Matlab
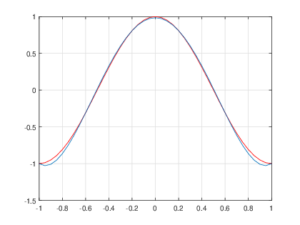
En esta sección veremos un ejemplo. Tomemos la función $f(t)=\cos{\pi t} \; , \: t\in[-1,1]$ con seis puntos espaciados uniformemente, $\{ -1, -0.6, -0.2, 0.2, 0.6, 1\}$, y su aproximación por un polinomio de Lagrange.
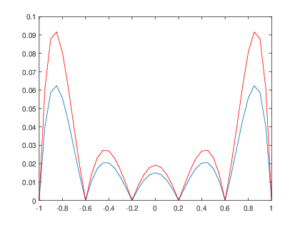
A continuación presentamos dos figuras construidas por medio de cuarenta y un puntos equiespaciados.
En la figura 2 podemos ver dos gráficas. La primera, en azul, describe el error puntual incurrido por la máquina al aproximar el coseno mientras que la segunda, en rojo, es la cota obtenida de manera analítica por medio del teorema del residuo de Cauchy para interpolaciones polinomiales. Es claro que el resultado númerico coincide con los desarrollos teóricos previos: la gráfica roja acota superiormente a la azul en todos sus puntos.
A continuación se presenta una tabla con los valores que se graficaron en las figuras anteriores.
| Coseno | Polinomio | Error | Cota del error | Coseno | Polinomio | Error | Cota del error |
|---|---|---|---|---|---|---|---|
| -1.0000 | -1.0000 | 0 | 0 | 0.9877 | 0.9738 | 0.0139 | 0.0179 |
| -0.9877 | -1.0277 | 0.0401 | 0.0609 | 0.9511 | 0.9402 | 0.0108 | 0.0139 |
| -0.9511 | -1.0099 | 0.0588 | 0.0879 | 0.8910 | 0.8850 | 0.0060 | 0.0077 |
| -0.8910 | -0.9534 | 0.0624 | 0.0917 | 0.8090 | 0.8090 | 0 | 0 |
| -0.8090 | -0.8648 | 0.0558 | 0.0808 | 0.7071 | 0.7136 | 0.0065 | 0.0084 |
| -0.7071 | -0.7504 | 0.0433 | 0.0618 | 0.5878 | 0.6004 | 0.0126 | 0.0164 |
| -0.5878 | -0.6161 | 0.0283 | 0.0398 | 0.4540 | 0.4715 | 0.0175 | 0.0230 |
| -0.4540 | -0.4673 | 0.0133 | 0.0184 | 0.3090 | 0.3294 | 0.0204 | 0.0269 |
| -0.3090 | -0.3090 | 0 | 0 | 0.1564 | 0.1769 | 0.0205 | 0.0273 |
| -0.1564 | -0.1461 | 0.0104 | 0.0141 | 0.0000 | 0.0172 | 0.0172 | 0.0231 |
| 0.0000 | 0.0172 | 0.0172 | 0.0231 | -0.1564 | -0.1461 | 0.0104 | 0.0141 |
| 0.1564 | 0.1769 | 0.0205 | 0.0273 | -0.3090 | -0.3090 | 0 | 0 |
| 0.3090 | 0.3294 | 0.0204 | 0.0269 | -0.4540 | -0.4673 | 0.0133 | 0.0184 |
| 0.4540 | 0.4715 | 0.0175 | 0.0230 | -0.5878 | -0.6161 | 0.0283 | 0.0398 |
| 0.5878 | 0.6004 | 0.0126 | 0.0164 | -0.7071 | -0.7504 | 0.0433 | 0.0618 |
| 0.7071 | 0.7136 | 0.0065 | 0.0084 | -0.8090 | -0.8648 | 0.0558 | 0.0808 |
| 0.8090 | 0.8090 | 0 | 0 | -0.8910 | -0.9534 | 0.0624 | 0.0917 |
| 0.8910 | 0.8850 | 0.0060 | 0.0077 | -0.9511 | -1.0099 | 0.0588 | 0.0879 |
| 0.9511 | 0.9402 | 0.0108 | 0.0139 | -0.9877 | -1.0277 | 0.0401 | 0.0609 |
| 0.9877 | 0.9738 | 0.0139 | 0.0179 | -1.0000 | -1.0000 | 0 | 0 |
| 1.0000 | 0.9850 | 0.0150 | 0.0192 |
Referencias
- Principles of Mathematical Analysis, Walter Rudin, McGraw Hill Education, India, 2013, página 107.
- Interpolation and Approximation, Philip J. Davis, Dover, USA, 1975, página 57.