Un Vistazo a la Teoría de Aproximación en la Mecánica Celeste
Las efemérides planetarias, en el contexto de la astronomía, son tablas que permiten determinar la posición de un objeto celeste o un satélite artificial con respecto a la Tierra en un momento dado, así como su trayectoria a lo largo del tiempo. Dichas tablas fueron herramientas indispensables para la navegación en siglos pasados y actualmente, siguen siendo utilizadas con frecuencia en proyectos de navegación e ingeniería espacial, así como en la predicción y el análisis de fenómenos astronómicos.
El primer registro que se tiene de la existencia de una efemérides es en la astronomía babilónica, alrededor de un milenio A.C.; desde entonces, estas herramientas han sido perfeccionadas por notables astrónomos de diversas civilizaciones. Entre las efemérides más destacables, por su uso y precisión a lo largo de la historia, están las siguientes: las Handy Tables de Ptolomeo, las cuales marcaron un precedente en el cálculo de las posiciones del Sol, la Luna y los planetas; las Tablas de Toledo, elaboradas por un grupo de astrónomos árabes en España en el año 1080 D.C. con base en la investigación astronómica islámica; las Tablas Alfonsinas del siglo XIII, que fueron ampliamente usadas por casi 300 años; las Tablas Pruténicas, las primeras efemérides que consideraban la teoría copernicana; y las Tablas Rudolfinas de Kepler, las cuales ya tomaban en cuenta el movimiento elíptico de los planetas.
Actualmente, las efemérides son generadas a partir de algoritmos que calculan las posiciones de los planetas, asteroides, cometas y satélites con una gran precisión. Los datos en estas tablas, además de ser capaces de estimar la trayectoria de un objeto, también permiten el cálculo de otras propiedades de los cuerpos celestes en un tiempo pasado o futuro, como su velocidad y aceleración orbital, el ángulo de elongación1, el diámetro aparente, el brillo y su tránsito planetario2.
El problema matemático detrás de generar una efeméride se resume en determinar una función que aproxime la posición del objeto celeste con respecto a la Tierra en un tiempo determinado. Para algunos lectores, no será sorpresa que la respuesta a este problema hace uso de la Teoría de Aproximación, en particular, de los polinomios de Chebyshev; por otro lado, quienes no están tan familiarizados con este campo del análisis matemático, descubrirán en los próximos párrafos por qué el uso de este método de aproximación es idóneo en este contexto.
Los polinomios de Chebyshev son una familia de polinomios ortogonales3 que, como se muestra a continuación, se construyen a partir de la fórmula de De Moivre, para valores de x en el intervalo cerrado [−1,1]. Tn(x) = cos (nθ), θ = arccos (x) A partir de esta relación, es posible definir de manera recursiva a estos polinomios como sigue T0(x) = 1, T1(x) = x, Tn + 1(x) = 2x * Tn(x) − Tn − 1(x) En particular, la representación gráfica de los primeros cuatro polinomios de Chebyshev es útil para entender la idea detrás de la fórmula recursiva dada anteriormente, ver Gráfica 1.
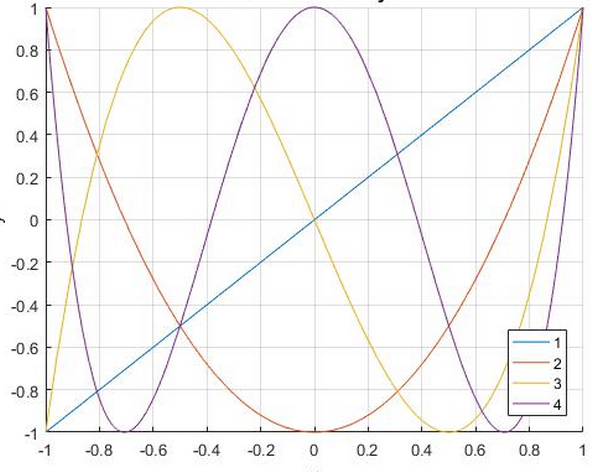
Además, analizando un poco más a fondo la imagen anterior y considerando la definición dada de los polinomios de Chebyshev, podemos llegar a las siguientes conclusiones: el grado de cada polinomio depende de n; el n-ésimo polinomio de Chebyshev tiene n raíces en [−1,1], las cuales corresponden a los puntos $x_n=\cos\left(\frac{(2n-1)\pi}{2n}\right)$; los valores extremos de este tipo de polinomios son 1 o -1.
Por otra parte, la razón por la cual los polinomios de Chebyshev son excelentes candidatos para la aproximación de una función, se debe a la siguiente proposición: $$P(x)=\frac{1}{2^{k-1}}*T_k(x)$$ es el polinomio mónico de grado k con mínima norma en el intervalo [−1,1]5.
Es decir, de todos los polinomios de grado k, el que alcanza un mínimo valor con respecto a la norma del supremo es proporcional al k-ésimo polinomio de Chebyshev. A su vez, esta propiedad implica que cualquier polinomio P de orden k, definido en el intervalo [−1,1], con coeficiente ak en el término de mayor orden, cumple con que $$\|P\|_\infty=\max_{x\in[-1,1]}(|P(x)|)\ge \frac{|a_k|}{2^{k-1}}$$ Las características y propiedades descritas anteriormente nos permiten hacer algunas observaciones importantes: en primer lugar, las raíces de estos polinomios, también conocidos como nodos de Chebyshev, pueden ser usados como nodos de interpolación para funciones a aproximar; por otra parte, determinando coeficientes apropiados, una combinación lineal de polinomios de Chebyshev es útil para la aproximación precisa6 de una función objetivo; finalmente, como los polinomios son funciones continuas y diferenciables, la primera y segunda derivada de los polinomios de Chebyshev nos dan información relevante sobre la función a la que aproximan.
Así pues, los polinomios de Chebyshev cumplen con una variedad de propiedades que los hacen únicos, versátiles y fáciles de aplicar en algoritmos numéricos. Por estas razones, esta familia de polinomios no solo aparece recurrentemente en la teoría e investigación, sino que ha sido usada en diversos problemas prácticos, tanto en el contexto de la computación, la física y la mecánica, así como en el contexto particular de la mecánica celeste.
A continuación, se describirá brevemente el uso que se le da a los polinomios de Chebyshev en el caso particular de las efemérides para conseguir una función que aproxima la posición de un cuerpo celeste a través del tiempo. En primer lugar, se considera la serie definida como $$p(x)=\sum_{n=0}^N p_n T_n(x),$$ con x ∈ [−1,1] y Tn el n-ésimo polinomio de Chebyshev, la cual describe la posición del objeto considerado en el tiempo. Esta función tiene por derivada a $$v(x)=\sum_{n=0}^N v_nT_n(x),$$ con vn = 0, función que aproxima a la velocidad a la que viaja el objeto. Finalmente, la segunda derivada de esta función está dada por $$a(x)=\sum_{n=0}^N a_n T_n(x),$$ con an = 0 = an − 1, que describe su aceleración.
De esta manera, determinando los coeficientes pn, es posible describir la posición, la velocidad y la aceleración de un determinado cuerpo celeste en un punto del tiempo t, a lo largo de un periodo [t0,t1], tomando $x=-a+2\frac{t-t_0}{t_1-t_0}$.
El método usual para determinar los coeficientes de una determinada función aproximante de la trayectoria de un cuerpo celeste particular no se discutirá en este artículo, dado que este se basa en la resolución de un sistema de ecuaciones que no se relaciona directamente con los polinomios de Chebyshev. Sin embargo, para aquellos lectores que estén interesados en dicho método, en el artículo “Numerical Representation of Planetary Ephemerides”, Newhall lo describe con detalle7.
Finalmente, a manera de conclusión de este artículo y teniendo en mente la información que el lector ha adquirido a lo largo del mismo, es pertinente mencionar que el centro de investigación NASA Jet Propulsion Laboratory ha desarrollado un sitio web, llamado JPL HORIZON System, que permite a cualquier cibernauta consultar efemérides de alta precisión, de diversos objetos celestes en el sistema solar8 a través de largos periodos de tiempo pasados y futuros. Estos resultados son generados al instante a partir de los métodos y herramientas matemáticos descritos anteriormente.
Para ilustrar la poderosa herramienta que esta página9 ofrece y reafirmar al lector que sí existen aplicaciones concretas a partir de las abstractas ideas con las que uno puede toparse en un curso de matemáticas, me tomé la libertad de elaborar las siguientes gráficas10 que describen la posición de Saturno en un periodo de 30 días11.
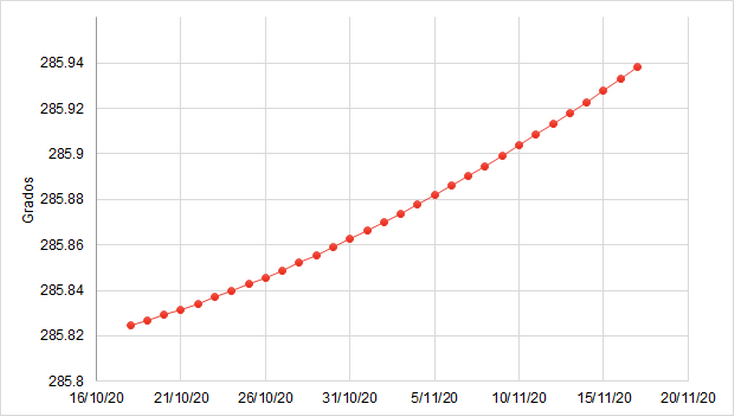
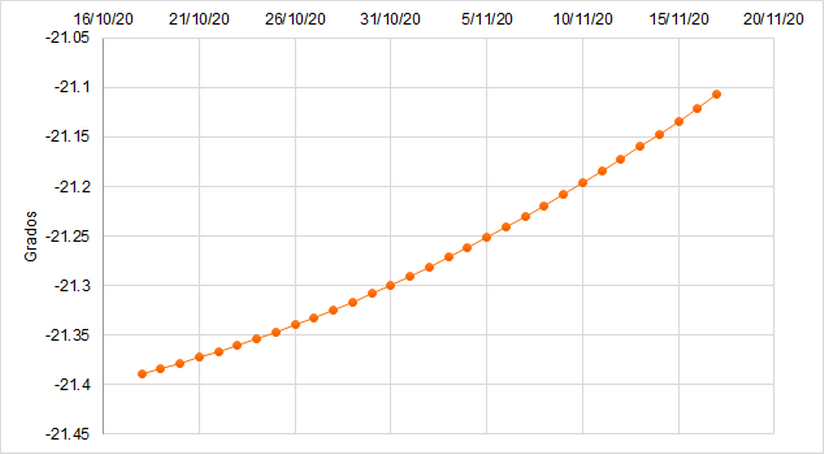
En astronomía, se conoce como elongación al ángulo formado entre un planeta y el sol con respecto a la Tierra.↩︎
Este término se refiere a cuando un astro se posiciona entre el Sol y la Tierra.↩︎
Dos funciones f, g son ortogonales si su producto escalar es nulo.↩︎
Para aquellos que estén interesados en explorar más a fondo la representación gráfica de los polinomios de Chebyshev, en la referencia correspondiente a Gráfica 1 podrán encontrar el código para generar esta imagen.↩︎
Un polinomio mónico de grado k es aquel cuyo coeficiente principal es 1.↩︎
Precisa en el sentido de que el error de aproximación con respecto a la función original es pequeño.↩︎
El enlace puede encontrarse en la lista de referencias.↩︎
Incluyendo a 10,166,065 asteroides, 3679 cometas, 209 satélites naturales, 8 planetas y el Sol.↩︎
Ambas gráficas fueron elaboradas a partir de los datos encontrados en https://ssd.jpl.nasa.gov/horizons.cgi#results↩︎
La ascensión recta y la declinación son coordenadas astrológicas que se miden en ángulos y se usan para determinar la posición de un objeto en el espacio con respecto a la Tierra.↩︎
Bibliografía
Wikipedia (2020). Ephemeris. https://en.wikipedia.org/wiki/Ephemeris
W. Thompson (1994). Chebyshev Polynomials: After the Spelling the Rest is Easy. Computers in Physics. Vol(8), 161-165. https://aip.scitation.org/doi/pdf/10.1063/1.4823278
A. Franco (2016). Polinomios de Chebyshev. http://www.sc.ehu.es/sbweb/fisica3/especial/chebyshev/chebyshev.html
F. Bach (2019). Polynomial magic I: Chebyshev polynomials. https://francisbach.com/chebyshev-polynomials/
E. Byhova, A. Tamarov (1978). Representation on planetary satellite ephemerides by Chebyshev polynomials. http://articles.adsabs.harvard.edu//full/1978SvAL….4..203B/0000203.000.html
X. Newhall (1989). Numerical Representation of Planetary Ephemerides. http://articles.adsabs.harvard.edu//full/1989CeMec..45..305N/0000305.000.html
/li>NASA. Jet Propulsion Laboratory (s.f). HORIZON System. https://ssd.jpl.nasa.gov/?horizons
