La esencia de las matemáticas reside en su libertad.
George Cantor
Introducción
Más allá de definir formalmente y demostrar nociones de dimensiones fractales, que es bastante tedioso, este artículo va a motivar la definición de dimensión de fractal o dimensión de Hausdorff de manera intuitiva y se mostrarán ejemplos de dos dimensiones fractales particularmente interesantes.
Un poco de historia
George Cantor, uno de los matemáticos más renombrados de finales del s.XIX, pasó mucho tiempo intentando demostrar la hipótesis del continuo y durante este tiempo llegó al famoso resultado que afirma que la cardinalidad del intervalo unitario en $\mathbb{R}$ es la misma que la cardinalidad de $\mathbb{R}$. Sabiendo esto, la comunidad metemática de la época se preguntó de la existencia de una función con dominio en el intervalo unitario y contradominio en una curva que cubra toda el área del cuadrado unitario. En 1890 el italiano Guiseppe Peano encontró una curva con tales caracteristicas y después de horas y horas de meditación decidió llamarla »Curva de Peano», al año siguiente el matemático David Hilbert descubre otra curva de llenado de espacio hoy conocida como »Curva de Hilbert». Pero, ¿qué tiene que ver esto con dimensiones no enteras? Para poder contestar la pregunta anterior primero debemos motivar la noción de dimensión de Hausdroff.
Dimensión de Hausdorff
Intuitivaemte, sabemos que una recta tiene una longitud mayor a cero y un área igual a cero, un cuadrado tiene un área mayor a cero y un volumen igual a cero. Ahora, como buenos matemáticos ¿tiene sentido por la longitud de un cuadrado? La respuesta es que sí, y que esta longitud es infinita. La afirmaciónn anterior nace del siguiente razonamiento: si en un cuadrado hay infinitas rectas que lo cubren, al sacar cada una de esas rectas del cuadrado y unirlas unas con otras llegaremos a una nueva recta de longitud infinita $($ver Figura $1)$.
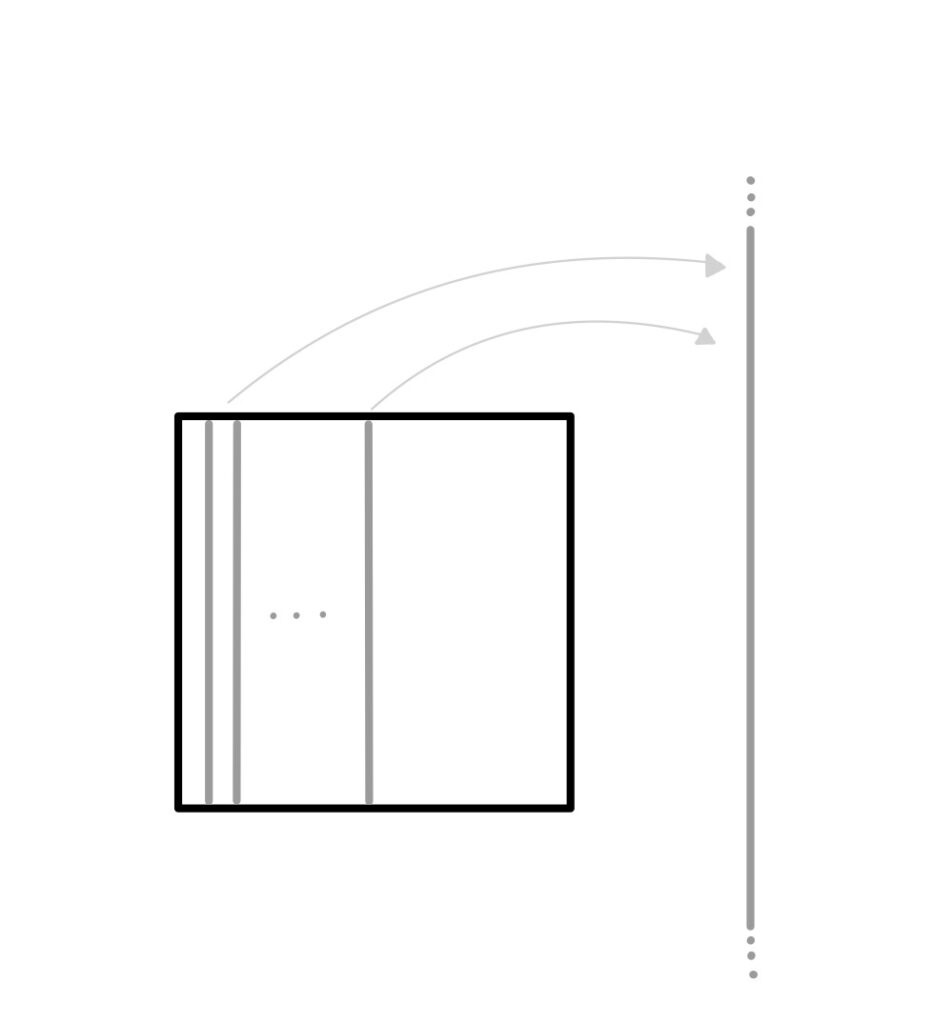
Lo mismo podemos decir sobre un cubo y su área, si laminamos el cubo en cuadrados terminamos con una cantidad infinita no numerable de cuadrados con área $1$ por lo que podemos unir los cuadrados arista con arista que generará un área infinita, por lo que el cubo tiene también un área infinita. La siguiente tabla resume lo explicado anteriormente.
| Longitud $(med_{1})$ | Área $(med_{2})$ | Volumen $(med_{3})$ | |
| Segmento $(Dim_{1})$ | $> 0$ | $0$ | $0$ |
| Cuadrado $(Dim_{2})$ | $\infty$ | $> 0$ | $0$ |
| Cubo $(Dim_{3})$ | $\infty$ | $\infty$ | $> 0$ |
Félix Hausdroff observó que para un objeto de dimensión $n$, con $n$ en los naturales, el valor de $med_{n-1}$ es infinito y el valor de $med_{n+1}$ es igual a cero. De cierta forma la dimensión del objeto es un parteaguas en los valores de las medidas. De lo anterior nace la noción de dimesión de Hausdroff, si cambiamos la $n$ por una $k$ en los reales, cuando $k$ es la dimensión de un objeto se cumple que $med_{\left \lfloor{k}\right \rfloor }$ es infinita y $med_{\left \lceil{k}\right \rceil }$ es cero.
Ahora bien, supongamos que queremos reescalar un objeto T por un factor de 2. Si el objeto es de una dimensión entonces la longitud será dos veces la longitud original. Si el objeto es un cuadrado entonces el área final será 4 veces el área original y si fuera un cubo el volumen final será 8 veces el volumen original. Generalizando el objeto a una dimensión $k$ y un factor de reescalamiento $x$ llegamos a la siguente igualdad:
\begin{equation}
med_{k}(r_{x}T) = x^{k}med_k(T)
\end{equation}
y es fácil ver que
\begin{equation}
med_{k}(r_{x}(T_1 + T_2)) = x^{k}med_k(T_1) + x^{k}med_k(T_2).
\end{equation}
De ahora en adelante, por simplicidad, llamaremos dimensión a la dimensión de Hausdorff.
Conjunto de Cantor
La construcción del conjunto de Cantor es como sigue:
- Tomar una recta de longitud 1.
- Dividir la recta en tres y eliminar segundo tercio.
- Repetir el segundo paso con los segmentos restantes.
La Figura 2 muestra 3 iteracciones de la construcción del conjunto.
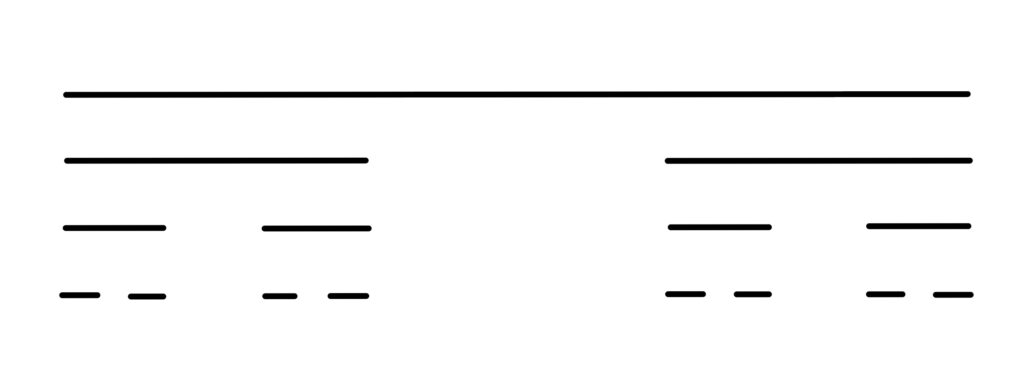
Dado que el ternario de Cantor está contenido en la recta, tiene sentido preguntarnos por la longitud del ternario en cada iteración.
| Paso | Cantidad de segmentos | Longitud individual | Longitud total |
| 1 | $2$ | $\dfrac{1}{3}$ | $\dfrac{2}{3}$ |
| 2 | $4$ | $\dfrac{1}{9}$ | $\dfrac{4}{9}$ |
| 3 | $8$ | $\dfrac{1}{27}$ | $\dfrac{8}{27}$ |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ |
| $n$ | $2^{n}$ | $\dfrac{1}{3^{n}}$ | $\dfrac{2^{n}}{3^{n}}$ |
Ahora, un punto tiene dimensión cero, al igual que una cantidad infinita numerable de puntos.
Se puede mostrar que el conjunto de cantor tiene una cantidad de puntos infinita no numerable por lo que concluimos que la dimensión del conjunto de Cantor es mayor a cero. Ahora en cuanto a la longitud, tomando el límite cuando $n$ tiende a infitinto vemos que la longitud total se va a cero entonces el conjunto tiene dimensión menor a uno y mayor a cero.
Sea $D$ la dimensión que buscamos y $T$ el conjunto de Cantor. En iteración cada uno de los segmentos se reescala a un factor de $1/3$ dos veces. Usando (1) y (2) después de la primer iteración tendremos:
$$med_{D}(T) = \left( \frac{1}{3} \right)^{D}med_D(T) + \left(\frac{1}{3}\right)^{D}med_D(T) = 2\left(\frac{1}{3}\right)^{D}med_D(T).$$
Como $med_D(T)$ no es cero ni infinito, pues $D$ es la dimensión, despejamos.
$$1 = 2\left(\frac{1}{3}\right)^{D}$$
entonces
$$D = ln(2)/ln(3) = 0.6309…$$
es la dimensión del conjunto de Cantor que, aparte de ser no entera, es irracional.
Curva de Hilbert
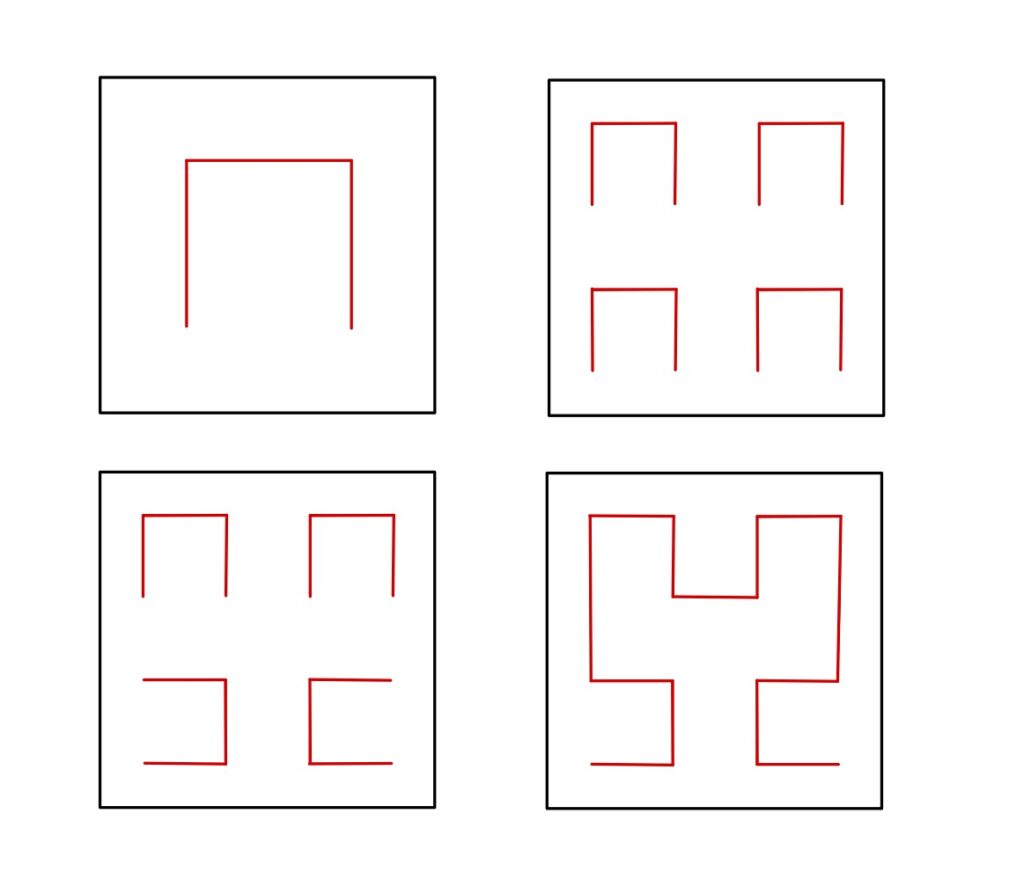
Ahora un ejemplo que a mi parecer es de los más interesantes, la curva de Hilbert. Una curva de llenado de espacio. La construcción de la curva de Hilbert es como sigue:
- Dividir al cuadrado unitario en cuatro cuadrados iguales y unir sus centros con una recta.
- Reescalar la recta y poner una copia en cada uno de los 4 sub-cuadrados.
- Rotar las figuras inferior izquierda y derecha noventa grados a la derecha e izquierda respectivamente.
- Unir con una recta las figuras.
- Repetir los pasos 2, 3 y 4 con la nueva curva.
En la Figura 3 se muestra el inicio de la construcción.
Y a continuación se muestran la segunda, tercera y cuarta iteración.
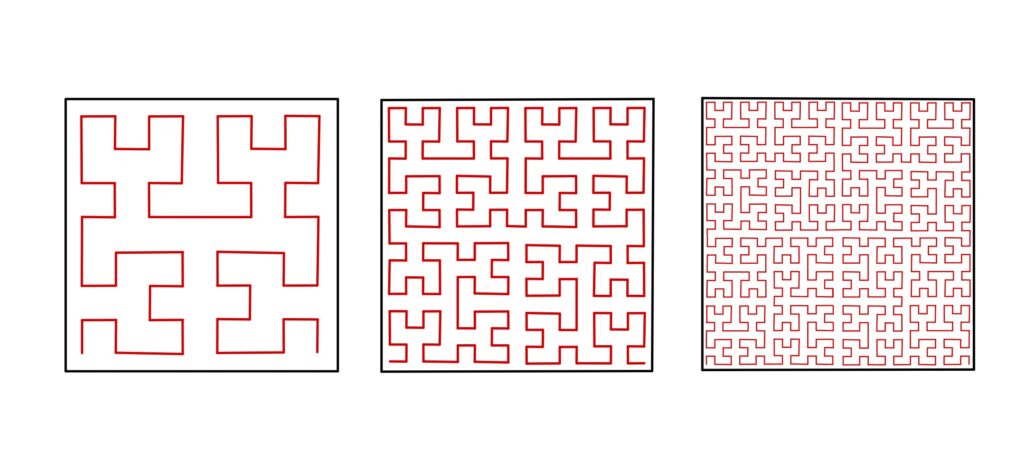
Ahora exploramos cómo va cambiando la longitud de la curva en cada iterarción.
| Paso | Cantidad de segmentos | Longitud individual | Longitud total |
| $1$ | $2^{2} -1$ | $\dfrac{1}{2}$ | $\dfrac{3}{2}$ |
| $2$ | $2^{4} -1$ | $\dfrac{1}{4}$ | $\dfrac{15}{4}$ |
| $3$ | $2^{6} -1$ | $\dfrac{1}{2^{3}}$ | $\dfrac{63}{8}$ |
| $4$ | $2^{8} -1$ | $\dfrac{1}{2^{4}}$ | $\dfrac{255}{16}$ |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ |
| $n$ | $2^{2n} -1$ | $\dfrac{1}{2^{n}}$ | $\dfrac{2^{2n} -1}{2^{n}}$ |
Tomamos el límite de la longitud total.
$$\lim_{x \to \infty} \frac{2^{2n} -1}{2^n} = \infty$$
por lo que concluimos que la dimensión de la curva de Hilbert es mayor a uno. Ahora, como la curva nunca sale del cuadrado unitario y tiene longitud infinita, basándonos en lo explicado sobre la Figura 1 intuimos
que la dimensión de la curva es 2 y su área es 1. En otras palabras, el área de los puntos del cuadrado que no cubre la curva de Hilbert es cero. Es decir, la curva de Hilbert es tan compleja que, de cierta forma, es una superficie. Lo anterior se puede demostar pero sale de los objetivos de este artículo.
Conclusión
El pensar que un objeto tiene una dimensión no entera o que existan curvas con área puede tomarse como algo bonito pero que se queda en plano teórico, increiblemente pasa todo lo contrario. Por ejemplo, la extención tridimensional del conjunto de Cantor, mejor conocido como esponja de Menger, ha motivado a usar dimensiones fractales para describir o caracerizar densidad de piedras y pordria usarse para describir estructuras biológicas complejas como los alveolos pulmonares. La curva de Hilbert, aparte de servir para tener un muy buen juego de snake, usualmente se usa para transformar sonido en imágenes y viceversa, esto porque al subir o bajar la sensibilidad del muestreo de un sonido, los puntos que representan cada sección de la onda sonora quedan cerca en la imagen, cosa que no pasaría si mapeáramos una onda a una imagen usando lineas rectas. La principal motivación de este artículo fue el primer libro de la bibliografía, que apliamente recomiendo si el lector disfrutó los temas tratados a lo largo de este texto.
1 Benoit Mandelbrot. «La Geometría Fractal de la Naturaleza.» W. H. Freeman and Company, 1982.
2«The Uncountability of the Unit Interval» 8/04/2021. https://arxiv.org/abs/1209.51
3«Introduction to dimension theory and fractal geometry: Fractal dimensions and measures» 5/04/2021. http://pi.math.cornell.edu/~erin/docs/dimension.pdf
4»Topological dimensions, Hausdorff dimensions and fractals» 2/04/2021. https://u.math.biu.ac.il/~megereli/final_topology.pdf
5Maria Isabel Binimelis Brasa. «Una nueva manera de ver el mundo-Geometría fractal}.» RBA, 2011.
6Gustavo Ernesto Piñeiro. «La esfera que quiso ser infinita-Las paradojas de la medida.» RBA, 2014.
Bibliografia
| 1. | ↑ | Benoit Mandelbrot. «La Geometría Fractal de la Naturaleza.» W. H. Freeman and Company, 1982. |
| 2. | ↑ | «The Uncountability of the Unit Interval» 8/04/2021. https://arxiv.org/abs/1209.51 |
| 3. | ↑ | «Introduction to dimension theory and fractal geometry: Fractal dimensions and measures» 5/04/2021. http://pi.math.cornell.edu/~erin/docs/dimension.pdf |
| 4. | ↑ | »Topological dimensions, Hausdorff dimensions and fractals» 2/04/2021. https://u.math.biu.ac.il/~megereli/final_topology.pdf |
| 5. | ↑ | Maria Isabel Binimelis Brasa. «Una nueva manera de ver el mundo-Geometría fractal}.» RBA, 2011. |
| 6. | ↑ | Gustavo Ernesto Piñeiro. «La esfera que quiso ser infinita-Las paradojas de la medida.» RBA, 2014. |
